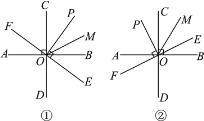
【题目】如图,已知O为直线AB上的一点,CD⊥AB于点O,PO⊥OE于点O,OM平分∠COE,点F在OE的反向延长线上.
(1)当OP在∠BOC内,OE在∠BOD内时,如图①所示,直接写出∠POM和∠COF之间的数量关系;
(2)当OP在∠AOC内且OE在∠BOC内时,如图②所示,试问(1)中∠POM和∠COF之间的数量关系是否发生变化?并说明理由.
参考答案:
【答案】(1)∠POM=![]() ∠COF,理由见解析;(2)∠POM=
∠COF,理由见解析;(2)∠POM=![]() ∠COF,理由见解析
∠COF,理由见解析
【解析】
(1)利用垂直的定义,CD⊥AB,PO⊥EO,等量代换得∠COP=∠BOE,利用角平分线的性质,得∠POM=![]() ∠POB=
∠POB=![]() (90°-∠POC),∠COF=90°-∠COP,得出结论;
(90°-∠POC),∠COF=90°-∠COP,得出结论;
(2)利用垂直的定义,同角的余角相等可得∠COP=∠AOF,可推出∠COP+∠COB=∠AOF+∠AOC,即∠BOP=∠COF,由对顶角相等得∠AOF=∠BOE=∠COP,利用角平分线的性质,得∠COP+∠COM=∠BOE+∠MOE,即∠POM=![]() ∠BOP,等量代换得出结论.
∠BOP,等量代换得出结论.
解:(1)∠POM=![]() ∠COF.
∠COF.
证明:∵CD⊥AB,
∴∠COP+∠BOP=90°,
∵OP⊥OE,
∴∠BOE+∠BOP=90°,
∴∠COP=∠BOE,
∵OM平分∠COE,
∴∠POM=∠MOB=![]() ∠POB=
∠POB=![]() (90°∠POC),
(90°∠POC),
∵∠COF=90°∠COP,
∴∠POM=![]() ∠COF;
∠COF;
(2)不发生变化.理由:∵CD⊥AB于点O,
∴∠AOP+∠COP=90°.
∵PO⊥OE于点O,
∴∠AOP+∠AOF=90°,
∴∠COP=∠AOF.
又∵∠AOC=∠COB=90°,
∴∠COP+∠COB=∠AOF+∠AOC,
即∠BOP=∠COF.
∵∠AOF=∠BOE,∴∠COP=∠BOE.
∵OM平分∠COE,∴∠COM=∠MOE,
∴∠COP+∠COM=∠BOE+∠MOE,
∴∠POM=![]() ∠BOP,
∠BOP,
∴∠POM=![]() ∠COF.
∠COF.
故答案为:(1)∠POM=![]() ∠COF,理由见解析;(2)∠POM=
∠COF,理由见解析;(2)∠POM=![]() ∠COF,理由见解析.
∠COF,理由见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学七、八年级各选派10名选手参加学校举办的“爱我荆门”知识竞赛,计分采用10分制,选手得分均为整数,成绩达到6分或6分以上为合格,达到9分或10分为优秀.这次竞赛后,七、八年级两支代表队选手成绩分布的条形统计图和成绩统计分析表如下,其中七年级代表队得6分、10分的选手人数分别为a,b.
队别
平均分
中位数
方差
合格率
优秀率
七年级
6.7
m
3.41
90%
n
八年级
7.1
7.5
1.69
80%
10%
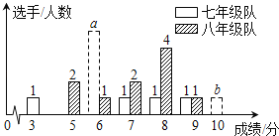
(1)请依据图表中的数据,求a,b的值;
(2)直接写出表中的m,n的值;
(3)有人说七年级的合格率、优秀率均高于八年级,所以七年级队成绩比八年级队好,但也有人说八年级队成绩比七年级队好.请你给出两条支持八年级队成绩好的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学进行社会调查,随机抽查了某小区的40户家庭的年收入(万元)情况,并绘制了如图不完整的频数直方图,每组包括前一个边界值,不包括后一个边界值.

(1)补全频数直方图.
(2)年收入的中位数落在哪一个收入段内?
(3)如果每一组年收入均以最低计算,这40户家庭的年平均收入至少为多少万元?
(4)如果该小区有1200户住户,请你估计该小区有多少家庭的年收入低于18万元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,添加以下条件,不能判定
,添加以下条件,不能判定 的是( )
的是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
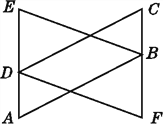
查看答案和解析>>【题目】如图,已知A,D,E三点共线,C,B,F三点共线,AB=CD,AD=CB,DE=BF,那么BE与DF之间有什么数量关系?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,工人师傅常用“卡钳”这种工具测定工件内槽的宽.卡钳由两根钢条AA′、BB′组成,O为AA′、BB′的中点.只要量出A′B′的长度,由三角形全等就可以知道工件内槽AB的长度.则判定△OAB≌△OA′B′的依据是( )

A. SASB. ASAC. SSSD. AAS
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中, ,
, ,
, .点
.点 从点
从点 出发,以
出发,以 的速度沿
的速度沿 向点
向点 运动,设点
运动,设点 的运动时间为
的运动时间为 .
.(1)
 ________
________ ;(用含
;(用含 的代数式表示)
的代数式表示)(2)如图1,当
 为何值时,
为何值时, ?并说明理由;
?并说明理由;
(3)如图2,当点
 从点
从点 开始运动,同时,点
开始运动,同时,点 从点
从点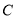 出发,以
出发,以 的速度沿
的速度沿 向点
向点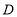 运动,当
运动,当 运动到点
运动到点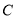 或点
或点 运动到点
运动到点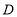 时运动停止.是否存在这样的
时运动停止.是否存在这样的 值,使得
值,使得 与
与 全等?若存在,请求出
全等?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
相关试题

