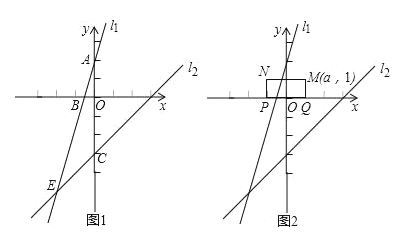
【题目】如图1,在直角坐标系中,一次函数的图象l![]() 与y轴交于点A(0 , 2),与一次函数y=x﹣3的图象l
与y轴交于点A(0 , 2),与一次函数y=x﹣3的图象l![]() 交于点E(m ,﹣5).
交于点E(m ,﹣5).
(1)m=__________;
(2)直线l![]() 与x轴交于点B,直线l
与x轴交于点B,直线l![]() 与y轴交于点C,求四边形OBEC的面积;
与y轴交于点C,求四边形OBEC的面积;
(3)如图2,已知矩形MNPQ,PQ=2,NP=1,M(a,1),矩形MNPQ的边PQ在x轴上平移,若矩形MNPQ与直线l![]() 或l
或l![]() 有交点,直接写出a的取值范围_____________________________
有交点,直接写出a的取值范围_____________________________
参考答案:
【答案】(1)-2;(2)![]() ;(3)
;(3)![]() ≤a≤
≤a≤![]() 或3≤a≤6.
或3≤a≤6.
【解析】
(1)根据点E在一次函数图象上,可求出m的值;
(2)利用待定系数法即可求出直线l1的函数解析式,得出点B、C的坐标,利用S四边形OBEC=S△OBE+S△OCE即可得解;
(3)分别求出矩形MNPQ在平移过程中,当点Q在l1上、点N在l1上、点Q在l2上、点N在l2上时a的值,即可得解.
解:(1)∵点E(m,5)在一次函数y=x3图象上,
∴m3=5,
∴m=2;
(2)设直线l1的表达式为y=kx+b(k≠0),
∵直线l1过点A(0,2)和E(2,5),
∴![]() ,解得
,解得 ,
,
∴直线l1的表达式为y=![]() x+2,
x+2,
当y=![]() x+2=0时,x=
x+2=0时,x=![]()
∴B点坐标为(![]() ,0),C点坐标为(0,3),
,0),C点坐标为(0,3),
∴S四边形OBEC=S△OBE+S△OCE=![]() ×
×![]() ×5+
×5+![]() ×2×3=
×2×3=![]() ;
;
(3)当矩形MNPQ的顶点Q在l1上时,a的值为![]() ;
;
矩形MNPQ向右平移,当点N在l1上时,![]() x+2=1,解得x=
x+2=1,解得x=![]() ,即点N(
,即点N(![]() ,1),
,1),
∴a![]() +2=
+2=![]() ;
;
矩形MNPQ继续向右平移,当点Q在l2上时,a的值为3,
矩形MNPQ继续向右平移,当点N在l2上时,x3=1,解得x=4,即点N(4,1),
∴a的值为4+2=6,
综上所述,当![]() ≤a≤
≤a≤![]() 或3≤a≤6时,矩形MNPQ与直线l1或l2有交点.
或3≤a≤6时,矩形MNPQ与直线l1或l2有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设二次函数y1,y2的图象的顶点分别为(a,b)、(c,d),当a=﹣c,b=2d,且开口方向相同时,则称y1是y2的“反倍顶二次函数”.
(1)请写出二次函数y=x2+x+1的一个“反倍顶二次函数”;
(2)已知关于x的二次函数y1=x2+nx和二次函数y2=nx2+x,函数y1+y2恰是y1﹣y2的“反倍顶二次函数”,求n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ACB=120°,以AC、BC为边向外作等边△ACF和等边△BCF,点P、M、N分别为AB、CF、CE的中点
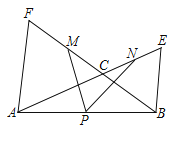
(1) 求证:PM=PN
(2) 求证:
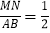
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

-
科目: 来源: 题型:
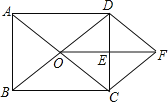
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为( )

A. 115° B. 120° C. 125° D. 130°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件之一能使平行四边形
 是菱形的为( )
是菱形的为( )①
 ;②
;②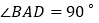 ;③
;③ ;④
;④ .
.
A. ①③ B. ②③ C. ③④ D. ①②③
相关试题

