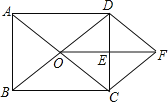
【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)根据两直线平行,内错角相等可得∠ODE=∠FCE,根据线段中点的定义可得CE=DE,然后利用“角边角”证明△ODE和△FCE全等;
(2)根据全等三角形对应边相等可得OD=FC,再根据一组对边平行且相等的四边形是平行四边形判断出四边形ODFC是平行四边形,根据矩形的对角线互相平分且相等可得OC=OD,然后根据邻边相等的平行四边形是菱形证明即可.
试题解析:(1)∵CF∥BD
∴∠DOE=∠CFE,
∵E是CD的中点,
∴CE=DE
在△ODE和△FCE中,
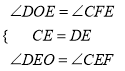 ,
,
∴△ODE≌△FCE(ASA)
∴OD=CF.
(2)由(1)知OD=CF ,
∵CF∥BD ,
∴四边形ODFC是平行四边形
在矩形ABCD中,OC=OD,
∴四边形ODFC是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=mx2+(2m+1)x+2(m为实数).

(1)请探究该函数图象与x轴的公共点个数的情况(要求说明理由);
(2)在图中给出的平面直角坐标系中分别画出m=﹣1和m=1的函数图象,并根据图象直接写出它们的交点坐标;
(3)探究:对任意实数m,函数的图象是否一定过(2)中的点,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是正方形ABCD内一点,点P到点A、B和D的距离分别为1,2
 ,
,  ,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q.
,△ADP沿点A旋转至△ABP′,连结PP′,并延长AP与BC相交于点Q. 
(1)求证:△APP′是等腰直角三角形;
(2)求∠BPQ的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,已知直线PQ∥MN,点A在直线PQ上,点C,D在直线MN上,连接AC,AD,∠PAC=50°,∠ADC=30°,AE平分∠PAD,CE平分∠ACD,AE与CE相交于点E.
(1)求∠AEC的度数;
(2)若将图①中的线段AD沿MN向右平移到A1D1如图②所示位置,此时A1E平分∠AA1D1,
CE平分∠ACD1,A1E与CE相交于E,∠PAC=50°,∠A1D1C=30°,求∠A1EC的度数;
(3)若将图①中的线段AD沿MN向左平移到A1D1如图③所示位置,其他条件与(2)相同,求此时∠A1EC的度数(直接写出结果).



-
科目: 来源: 题型:
查看答案和解析>>【题目】某停车场收费标准分为中型汽车和小型汽车两种,某两天这个停车场的收费情况如下表:
中型汽车数量
小型汽车数量
收取费用
第一天
15辆
35辆
360元
第二天
18辆
20辆
300元
(1)中型汽车和小型汽车的停车费每辆多少元?
(2)某天停车场共停车70辆,若收取的停车费用高于500元,则中型汽车至少有多少辆?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
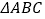 中,
中,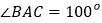 ,
,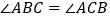 ,点
,点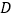 在直线
在直线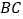 上运动(不与点
上运动(不与点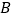 、
、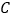 重合),点
重合),点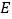 在射线
在射线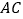 上运动,且
上运动,且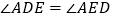 ,设
,设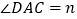 .
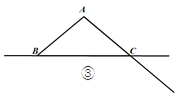
.(1)如图①,当点
 在边
在边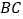 上时,且
上时,且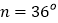 ,则
,则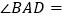 _______,
_______,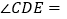 _______;
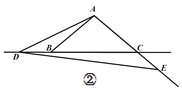
_______;(2)如图②,当点
 运动到点
运动到点 的左侧时,其他条件不变,请猜想
的左侧时,其他条件不变,请猜想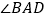
和
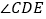 的数量关系,并说明理由;
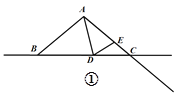
的数量关系,并说明理由;(3)当点
 运动到点C的右侧时,其他条件不变,
运动到点C的右侧时,其他条件不变,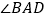 和
和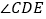 还满足(2)
还满足(2)中的数量关系吗?请画出图形,并说明理由.
相关试题

