【题目】已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点. 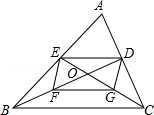
(1)求证:四边形DEFG是平行四边形;
(2)如果△ABC中AB=AC,四边形DEFG的形状是(直接写出结果).
参考答案:
【答案】
(1)证明:∵D、E分别为AC、AB的中点
∴ED∥BC,ED= ![]() BC.
BC.
同理FG∥BC,FG= ![]() BC,
BC,
∴ED∥FG,ED=FG,
∴四边形DEFG是平行四边形
(2)矩形
【解析】解:(2)如图1,当AB=AC时,DEFG变成矩形. 理由如下:
连接AO并延长交BC于点M.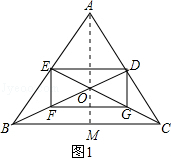
∵三角形的三条中线相交于同一点,△ABC的中线BD、CE交于点O,
∴M为BC的中点,
当AB=AC时,AM⊥BC,
∵E,F,G分别是AB,OB,OC的中点,
∴EF∥AO,FG∥BC,
∴EF⊥FG;
∴四边形EFGH是矩形.
所以答案是:矩形.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对三角形中位线定理的理解,了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门打开的宽度BC为2米,以下哪辆车可以通过?(栏杆宽度,汽车反光镜忽略不计)(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.车辆尺寸:长×宽×高)( )
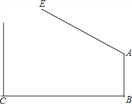
A. 宝马Z4(4200mm×1800mm×1360mm) B. 奔驰smart(4000mm×1600mm×1520mm)
C. 大众朗逸(4600mm×1700mm×1400mm) D. 奥迪A6L(4700mm×1800mm×1400mm)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a2=4,那么a=( )
A.2
B.﹣2
C.±2
D.±4 -
科目: 来源: 题型:
查看答案和解析>>【题目】若一个角为30°,则它的余角的度数为( )
A. 30° B. 60° C. 150° D. 170°
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式计算正确的是( )
A. 3ab﹣2ab=ab B. 5y2﹣4y2=1 C. 2a+3b=5ab D. 3+x=3x
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先画出了如图的四边形ABCD,并写出了如下不完整的已知和求证.
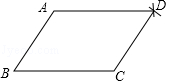
(1)在方框中填空,以补全已知和求证; 已知:如图,在四边形ABCD中,BC=AD, .
求证:四边形ABCD是 .
(2)写出证明过程: -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4
x+4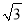 与x轴、y轴分别交于A、B两点, ∠ABC=60°,BC与x轴交于点C.动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿C-B-A向点A运动(不与C、A重合) ,动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.若当△APQ的面积最大时,y轴上有一点M,第二象限内存在一点N,使以A、Q、M、N为顶点的四边形为菱形, 则点N的坐标为_________
与x轴、y轴分别交于A、B两点, ∠ABC=60°,BC与x轴交于点C.动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发沿C-B-A向点A运动(不与C、A重合) ,动点P的运动速度是每秒1个单位长度,动点Q的运动速度是每秒2个单位长度.若当△APQ的面积最大时,y轴上有一点M,第二象限内存在一点N,使以A、Q、M、N为顶点的四边形为菱形, 则点N的坐标为_________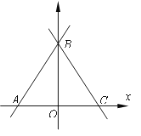
相关试题

