【题目】已知边长为m的正方形面积为12,则下列关于m的说法中,错误的是( ) ①m是无理数;
②m是方程m2﹣12=0的解;
③m满足不等式组 ![]() ;
;
④m是12的算术平方根.
A.①②
B.①③
C.③
D.①②④
参考答案:
【答案】C
【解析】解:∵边长为m的正方形面积为12, ∴m2=12,
∴m=2 ![]() ,
,
∵ ![]() 是一个无理数,
是一个无理数,
∴m是无理数,
∴结论①正确;
∵m2=12,
∴m是方程m2﹣12=0的解,
∴结论②正确;
∵不等式组 ![]() 的解集是4<m<5,m=2
的解集是4<m<5,m=2 ![]() <2×2=4,
<2×2=4,
∴m不满足不等式组 ![]() ,
,
∴结论③不正确;
∵m2=12,而且m>0,
∴m是12的算术平方根,
∴结论④正确.
综上,可得
关于m的说法中,错误的是③.
故选:C.
【考点精析】认真审题,首先需要了解无理数(在理解无理数时,要抓住“无限不循环”这个要点,归纳起来有四类:(1)开方开不尽的数;(2)有特定意义的数,如圆周率π,或化简后含有π的数;(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数,如sin60o等),还要掌握不等式的解集(一个含有未知数的不等式的所有解,组成这个不等式的解集(即未知数的取值范围))的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在解决线段数量关系问题中,如果条件中有角平分线,经常采用下面构造全等三角形的解决思路.如:在图1中,若
 是
是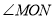 的平分线
的平分线 上一点,点
上一点,点 在
在 上,此时,在
上,此时,在 截取
截取 ,连接
,连接 ,根据三角形全等的判定
,根据三角形全等的判定 ,容易构造出全等三角形⊿
,容易构造出全等三角形⊿ 和⊿
和⊿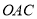 ,参考上面的方法,解答下列问题:
,参考上面的方法,解答下列问题:
如图2,在非等边⊿
 中,
中,  ,
,  分别是
分别是 的平分线,且
的平分线,且 交于点
交于点 .求证:
.求证:  .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列解答过程:如图甲,AB∥CD,探索∠P与∠A,∠C之间的关系.
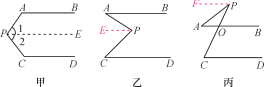
解:过点P作PE∥AB.
∵AB∥CD,
∴PE∥AB∥CD(平行于同一条直线的两条直线互相平行).
∴∠1+∠A=180°(两直线平行,同旁内角互补),
∠2+∠C=180°(两直线平行,同旁内角互补).
∴∠1+∠A+∠2+∠C=360°.
又∵∠APC=∠1+∠2,
∴∠APC+∠A+∠C=360°.
如图乙和图丙,AB∥CD,请根据上述方法分别探索两图中∠P与∠A,∠C之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,BE平分∠ABC,交AC边于点E,ED⊥AB,垂足为D.若△ABC的周长为12,△ADE的周长为6,则BC的长为( )

A. 3 B. 4 C. 5 D. 6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于
 AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( ) 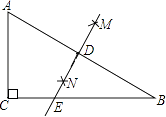
A.2
B.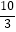
C.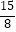
D.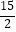
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列图案均是长度相同的火柴按一定的规律拼搭而成:第1个图案需7根火柴,第2个图案需13根火柴,…,依此规律,第11个图案需( )根火柴.
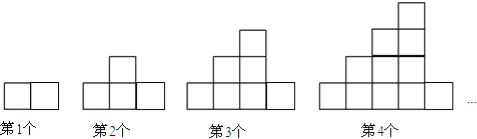
A. 156 B. 157 C. 158 D. 159
相关试题

