【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)△ACE是直角三角形,理由见解析.
【解析】分析:(1)根据四边形ABCD和四边形BPEF是正方形,证明△APE≌△CFE;(2)分别判断△ABC,△APE是等腰直角三角形得∠CAE=90°.
详解:(1)∵四边形ABCD和四边形BPEF是正方形,
∴AB=BC,BP=BF,∴AP=CF,
在△APE和△CFE中,
AP=CF,∠P=∠F,PE=EF,
∴△APE≌△CFE,
∴EA=EC;
(2)∵P为AB的中点,
∴PA=PB,又PB=PE,
∴PA=PE,
∴∠PAE=45°,又∠DAC=45°,
∴∠CAE=90°,即△ACE是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
(1)求证:四边形PMEN是平行四边形;
(2) 当AP为何值时,四边形PMEN是菱形?并给出证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.
(1)若AB=12 cm,则MN的长度是______cm;
(2)若AC=3 cm,CP=1 cm,求线段PN的长度.
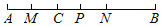
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示①,OP为一条拉直的细线,A,B两点在OP上,且OA:AP=1:3,OB:BP =3:5.若先固定B点,将OB折向BP,使得OB重叠在BP上,如图13-②,再从图②的A点及与A点重叠处一起剪开,使得细线分成三段,求三段细线由小到大的长度比.

-
科目: 来源: 题型:
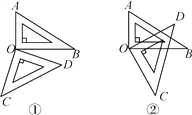
查看答案和解析>>【题目】如图①所示,将一副三角尺的直角顶点重合在点O处.
(1)①∠AOD和∠BOC相等吗?(不要求说明理由)
②∠AOC和∠BOD在数量上有何种关系?(不要求说明理由)
(2)若将这副三角尺按如图②摆放,三角尺的直角顶点重合在点O处.
①∠AOD和∠BOC相等吗?说明理由;
②∠AOC和∠BOD在数量上有何种关系?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填空:
(a﹣b)(a+b)=
(a﹣b)(a2+ab+b2)=
(a﹣b)(a3+a2b+ab2+b3)=
(2)猜想:(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)= (其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:39﹣38+37﹣…+33﹣32+3.
相关试题

