【题目】已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC.
求证:∠1与∠2互余.

参考答案:
【答案】证明见解析.
【解析】
试题分析:先根据AB∥CD得出∠ABD+∠BDC=180°,再根据BE、DE分别平分∠ABD、∠BDC可知∠EBD+∠EDB=90°,由三角形内角和定理可知,∠BED=90°,再根据平角的定义即可得出结论.
试题解析:∵AB∥CD,EF∥AB,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠FED=∠CDE,
且∠ABD+∠BDC=180°.
又∵BE、DE 分别平分∠ABD,∠CDB,
∴∠BEF=![]() ∠ABD,∠FED=
∠ABD,∠FED=![]() ∠BDC,
∠BDC,
∴∠BEF+∠FED=90°,
∴∠1+∠2=90°,
∴∠1与∠2互余.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列数据是某班六位同学定点投篮(每人投10个)的情况,投进篮筐的个数为6,9,8,4,0,3,这组数据的平均数、中位数和极差分别是
A.6,6,9 B.6,5,9 C.5,6,6 D.5,5,9
-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年十一黄金周商场大促销,某店主计划从厂家采购高级羽绒服和时尚皮衣两种产品共20件,高级羽绒服的采购单价y1(元/件)与采购数量x1(件)满足y1=﹣20x1+1500(0<x1≤20,x1为整数);时尚皮衣的采购单价y2(元/件)与采购数量x2(件)满足y2=﹣10x2+1300(0<x2≤20,x2为整数).
(1)经店主与厂家协商,采购高级羽绒服的数量不少于时尚皮衣数量,且高级羽绒服采购单价不低于1240元,问该店主共有几种进货方案?
(2)该店主分别以1760元/件和1700元/件的销售出高级羽绒服和时尚皮衣,且全部售完,则在(1)问的条件下,采购高级羽绒服多少件时总利润最大?并求最大利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是将菱形ABCD以点O为中心按顺时针方向分别旋转90°,180°,270°后形成的图形。若
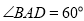 ,AB=2,则图中阴影部分的面积为______.
,AB=2,则图中阴影部分的面积为______.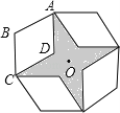
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索发现:
如图所示,已知AB∥CD,分别写出下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选二个加以说明.

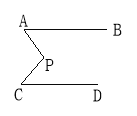
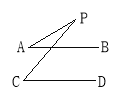

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°.
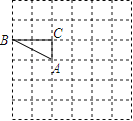
(1)画出旋转后的△AB′C′;
(2)以点C为坐标原点,线段BC、AC所在直线分别为x轴,y轴建立直角坐标系,请直接写出点B′的坐标 ;
(3)写出△ABC在旋转过程中覆盖的面积 .
-
科目: 来源: 题型:
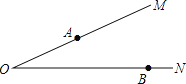
查看答案和解析>>【题目】如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
A.3 B.3
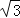 C.2 D.2
C.2 D.2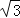
相关试题

