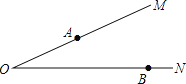
【题目】如图,∠MON=20°,A、B分别为射线OM、ON上两定点,且OA=2,OB=4,点P、Q分别为射线OM、ON两动点,当P、Q运动时,线段AQ+PQ+PB的最小值是( )
A.3 B.3![]() C.2 D.2
C.2 D.2![]()
参考答案:
【答案】D
【解析】
试题分析:首先作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,可求得AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,然后由特殊角的三角函数值,判定∠OA′B′=90°,再利用勾股定理求得答案.
解:作A关于ON的对称点A′,点B关于OM的对称点B′,连接A′B′,交于OM,ON分别为P,Q,连接OA′,OB′,
则PB′=PB,AQ=A′Q,OA′=OA=2,OB′=OB=4,∠MOB′=∠NOA′=∠MON=20°,
∴AQ+PQ+PB=A′Q+PQ+PB′=A′B′,∠A′OB′=60°,
∵cos60°=![]() ,
,![]() =
=![]() ,
,
∴∠OA′B′=90°,
∴A′B′=![]() =2
=2![]() ,
,
∴线段AQ+PQ+PB的最小值是:2![]() .
.
故选D.
-
科目: 来源: 题型:
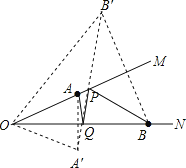
查看答案和解析>>【题目】已知:如图,AB∥CD,EF∥AB,BE、DE分别平分∠ABD、∠BDC.
求证:∠1与∠2互余.

-
科目: 来源: 题型:
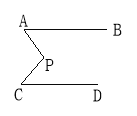
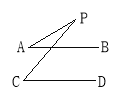
查看答案和解析>>【题目】探索发现:
如图所示,已知AB∥CD,分别写出下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选二个加以说明.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的方格纸上将△ABC绕点A顺时针旋转90°.
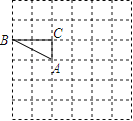
(1)画出旋转后的△AB′C′;
(2)以点C为坐标原点,线段BC、AC所在直线分别为x轴,y轴建立直角坐标系,请直接写出点B′的坐标 ;
(3)写出△ABC在旋转过程中覆盖的面积 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题:若x2=9,则x=3是____________命题.(填 “真”或“假”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算结果正确的是( )
A. (﹣2x2)3=﹣6x6 B. x2x3=x6 C. 6x4÷3x3=2x D. x2+x3=2x5
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a﹣2b+3=0,则代数式5+2b﹣a的值是( )
A.2
B.4
C.6
D.8
相关试题

