【题目】如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,则∠BOC= °,∠DOE= °;
(2)若∠AOC=m°,∠AOB=n°(n>m),则∠BOC= °,∠DOE= °;
(3)猜想:∠DOE与∠BOC有怎样的数量关系?并说明理由.

参考答案:
【答案】(1)90,45;(2)(n﹣m),![]() (n﹣m);(3)∠DOE=
(n﹣m);(3)∠DOE=![]() ∠BOC.
∠BOC.
【解析】
(1) 依据∠AOC=20°, ∠AOB=110°, 可得∠BOC=110° -20°=90°; 再根据OD、 OE分别平分∠AOB, ∠AOC, 即可得到∠DOE的度数;
(2) 依据∠AOC= m°, ∠AOB= n°,可得∠BOC= n°- m°= (n°- m°); 再根据OD、 OE分别平分∠AOB、 ∠AOC, 可得∠AOD= ![]() n°, LAOE=
n°, LAOE= ![]() m°,进而得出∠DOE的度数;
m°,进而得出∠DOE的度数;
(3) 依据OD、 OE分别平分∠AOB、 ∠AOC, 即可得出∠AOD=![]() ∠AOB, ∠AOE=
∠AOB, ∠AOE=![]() ∠AOC, 进而得到∠DOE=∠AOD-∠AOE=
∠AOC, 进而得到∠DOE=∠AOD-∠AOE= ![]() (∠AOB-∠AOC) =
(∠AOB-∠AOC) =![]() ∠BOC.
∠BOC.
解:(1)
∵∠AOC=20°,∠AOB=110°,
∴∠BOC=110°﹣20°=90°;
∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=55°,∠AOE=10°,
∴∠DOE=55°﹣10°=45°;
故答案为:90,45;
(2)∵∠AOC=m°,∠AOB=n°,
∴∠BOC=n°﹣m°=(n﹣m)°;
∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=![]() n°,∠AOE=
n°,∠AOE=![]() m°,
m°,
∴∠DOE=∠AOD﹣∠AOE=![]() (n﹣m)°;
(n﹣m)°;
故答案为:(n﹣m),![]() (n﹣m);
(n﹣m);
(3)∠DOE=![]() ∠BOC.
∠BOC.
证明:∵OD、OE分别平分∠AOB、∠AOC,
∴∠AOD=![]() ∠AOB,∠AOE=∠AOC,
∠AOB,∠AOE=∠AOC,
∴∠DOE=∠AOD﹣∠AOE=![]() (∠AOB﹣∠AOC)=
(∠AOB﹣∠AOC)=![]() ∠BOC.
∠BOC.
-
科目: 来源: 题型:
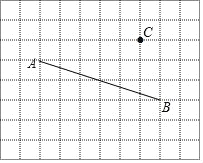
查看答案和解析>>【题目】利用网格画图:
(1)过点C画AB的平行线;
(2)过点C画AB的垂线,垂足为E;
(3)连接CA、CB,在线段CA、CB、CE中, 线段最短,理由: ;
(4)点C到直线AB的距离是线段的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为增强公民的节约意识,合理利用天然气资源,某市自1月1日起对市区民用管道天然气价格进行调整,实行阶梯式气价,调整后的收费价格如表所示:
每月用气量
单价(元/m3)
不超出80m3的部分
2.5
超出80m3不超出130m3的部分
a
超出130m3的部分
a+0.5
(1)若甲用户3月份用气125m3,缴费335元,求a的值;
(2)在(1)的条件下,若乙用户3月份缴费392元,则乙用户3月份的用气量是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于的一次函数
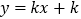 的图象可能是( )
的图象可能是( )A.
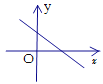
B.
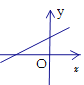
C.

D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上点A表示的数为10,点B在点A左边,且AB=18.动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
(1)写出数轴上点B表示的数,点P表示的数(用含t的代数式表示);
(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发.
①问点P运动多少秒时追上点Q?
②问点P运动多少秒时与点Q相距4个单位长度?并求出此时点P表示的数;
(3)若点P、Q以(2)中的速度同时分别从点A、B向右运动,同时点R从原点O以每秒7个单位的速度向右运动,是否存在常数m,使得2QR+3OP﹣mOR为定值,若存在请求出m值以及这个定值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB分别交y轴、x轴于A、B两点,OA=2,tan∠ABO=
 ,抛物线y=﹣x2+bx+c过A、B两点.
,抛物线y=﹣x2+bx+c过A、B两点.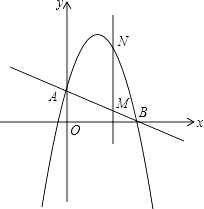
(1)求直线AB和这个抛物线的解析式;
(2)设抛物线的顶点为D,求△ABD的面积;
(3)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN的长度l有最大值?最大值是多少?
相关试题

