【题目】某校为了在九月份迎接高一年级的新生,决定将学生公寓楼重新装修,现学校招用了甲、乙两个工程队.若两队合作,8天就可以完成该项工程;若由甲队先单独做3天后,剩余部分由乙队单独做需要18天才能完成.
(1)求甲、乙两队工作效率分别是多少?
(2)甲队每天工资3000元,乙队每天工资1400元,学校要求在12天内将学生公寓楼装修完成,若完成该工程甲队工作m天,乙队工作n天,求学校需支付的总工资w(元)与甲队工作天数m(天)的函数关系式,并求出m的取值范围及w的最小值.
参考答案:
【答案】(1)甲、乙两队工作效率分别是![]() 和
和![]() .(2)6≤m≤12.34800元.
.(2)6≤m≤12.34800元.
【解析】
试题分析:(1)设甲队单独完成需要x天,乙队单独完成需要y天.列出分式方程组即可解决问题;
(2)设乙先工作x天,再与甲合作正好如期完成.则![]() ,解得x=6.由此可得m的范围,因为乙队每天的费用小于甲队每天的费用,所以让乙先工作6天,再与甲合作6天正好如期完成,此时费用最小;
,解得x=6.由此可得m的范围,因为乙队每天的费用小于甲队每天的费用,所以让乙先工作6天,再与甲合作6天正好如期完成,此时费用最小;
试题解析:(1)设甲队单独完成需要x天,乙队单独完成需要y天.
由题意 ,解得
,解得![]() ,
,
经检验![]() 是分式方程组的解,
是分式方程组的解,
∴甲、乙两队工作效率分别是![]() 和
和![]() .
.
(2)设乙先工作x天,再与甲合作正好如期完成.
则![]() ,解得x=6.
,解得x=6.
∴甲工作6天,
∵甲12天完成任务,
∴6≤m≤12.
∵乙队每天的费用小于甲队每天的费用,
∴让乙先工作6天,再与甲合作6天正好如期完成,此时费用最小,
∴w的最小值为12×1400+6×3000=34800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(﹣3)0等于( )
A.1
B.﹣1
C.﹣3
D.0 -
科目: 来源: 题型:
查看答案和解析>>【题目】端午节期间,某校“慈善小组”筹集到1240元善款,全部用于购买水果和粽子,然后到福利院送给老人,决定购买大枣粽子和普通粽子共20盒,剩下的钱用于购买水果,要求购买水果的钱数不少于180元但不超过240元.已知大枣粽子比普通粽子每盒贵15元,若用300元恰好可以买到2盒大枣粽子和4盒普通粽子.
(1)请求出两种口味的粽子每盒的价格;
(2)设买大枣粽子x盒,买水果共用了w元. ①请求出w关于x的函数关系式;
②求出购买两种粽子的可能方案,并说明哪一种方案使购买水果的钱数最多. -
科目: 来源: 题型:
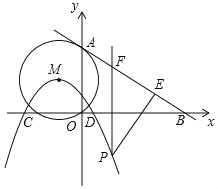
查看答案和解析>>【题目】如图,⊙M的圆心M(﹣1,2),⊙M经过坐标原点O,与y轴交于点A,经过点A的一条直线l解析式为:y=﹣
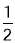 x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).
x+4与x轴交于点B,以M为顶点的抛物线经过x轴上点D(2,0)和点C(﹣4,0).(1)求抛物线的解析式;
(2)求证:直线l是⊙M的切线;
(3)点P为抛物线上一动点,且PE与直线l垂直,垂足为E,PF∥y轴,交直线l于点F,是否存在这样的点P,使△PEF的面积最小?若存在,请求出此时点P的坐标及△PEF面积的最小值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个圆柱和一个圆锥的底面圆的半径与高都分别相等,它们的体积差是24立方厘米,圆柱的体积是______立方厘米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算a2(a2)3的结果是( )
A.a7B.a10C.a8D.a12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( )
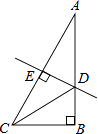
A.2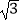
B.2
C.4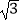
D.4
相关试题

