【题目】如图,在梯形ABCD中,AD∥BC,BC=2AD,点F、G分别是边BC、CD的中点,连接AF、FG,过点D作DE∥FG交AF于点E. 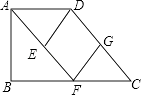
(1)求证:△AED≌△CGF;
(2)若梯形ABCD为直角梯形,∠B=90°,判断四边形DEFG是什么特殊四边形?并证明你的结论;
(3)若梯形ABCD的面积为a(平方单位),则四边形DEFG的面积为(平方单位).(只写结果,不必说理)
参考答案:
【答案】
(1)证明:∵BC=2AD,点F为BC的中点,
∴CF=AD.
又∵AD∥BC,
∴四边形AFCD是平行四边形,
∴∠DAE=∠C,AF∥DC,
∴∠AFG=∠CGF.
∵DE∥GF,
∴∠AED=∠AFG,
∴∠AED=∠CGF
∴△AED≌△CGF;
(2)解:结论:四边形DEFG是菱形.
证明如下:连接DF.
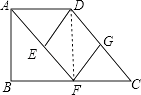
由(1)得AF∥DC,
又∵DE∥GF,
∴四边形DEFG是平行四边形.
∵AD∥BC,AD=BF= ![]() BC,
BC,
∴四边形ABFD是平行四边形,
又∵∠B=90°,
∴四边形ABFD是矩形,
∴∠DFC=90°,
∵点G是CD的中点,
∴FG=DG= ![]() CD,
CD,
∴四边形DEFG是菱形;
(3)![]() a
a
【解析】(3)四边形DEFG的面积=梯形ABCD的面积﹣S△ABF﹣2S△CFG ,
∵梯形ABCD的面积为a,
∴四边形DEFG的面积为 ![]() a;
a;
【考点精析】根据题目的已知条件,利用梯形的定义的相关知识可以得到问题的答案,需要掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出
 关于
关于 轴对称的
轴对称的 .
.(2)写出点
 的坐标(直接写答案).
的坐标(直接写答案).A1_____________,B1______________,C1______________
-
科目: 来源: 题型:
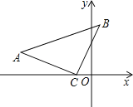
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90°,AC=BC,C点坐标为(﹣3,0),A点坐标为(﹣8,4),则B点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G.

(1)求证:△CEG是等边三角形;
(2)若矩形的一边AD=3,求另一边AB的长. -
科目: 来源: 题型:
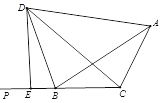
查看答案和解析>>【题目】如图,BD是△ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE的长为 _____________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别是C,D.求证:OE垂直平分CD.
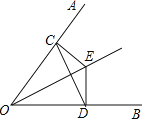
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;
(2)已知AC=20,AB=12,求CF的长.
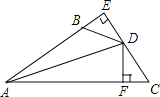
相关试题

