【题目】如图,现将一张矩形ABCD的纸片一角折叠,若能使点D落在AB边上F处,折痕为CE,恰好∠AEF=60°,延长EF交CB的延长线于点G. 
(1)求证:△CEG是等边三角形;
(2)若矩形的一边AD=3,求另一边AB的长.
参考答案:
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC即AD∥GC,
∴∠G=∠AEF=60°,
由折叠可知:∠CED=∠CEG,而∠GED=180°﹣∠AEF=120°
∴∠GEC=∠CED= ![]() ∠GED=60°即∠G=∠GEC=60°,
∠GED=60°即∠G=∠GEC=60°,
∴△CEG是等边三角形;
(2)解:∵四边形ABCD是矩形∴∠A=∠D=90°,AB=CD,
由(1)可知∠AEF=∠CED=60°,∴∠AFE=∠DCE=30°,
∴EF=2AE,CE=2DE.设AE=x,则EF=2x,ED=EF=2x,
∴AD=x+2x=3,CE=4x,解得,x=1,DE=2,CE=4,
在Rt△CDE中,CD= ![]()
∴AB=2 ![]() .
.
【解析】(1)由折叠可知∠DEC=∠FEC,已知∠AEF=60°,可知∠DEC=∠FEC=60°,由AD∥GC,可知∠G=∠AEF=60°,故有∠G=∠FEC=60°,所以△CEG是等边三角形;(2)在Rt△AEF中,∠AEF=60°,设AE=x,则EF=2x,由折叠的性质得ED=EF=2x,根据AE+ED=AD,列方程求x,在Rt△CDE中,DE=2,∠DEC=60°,可得CE=2DE=4,利用勾股定理可求CD,即AB的长.
【考点精析】解答此题的关键在于理解翻折变换(折叠问题)的相关知识,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)与x轴交于点A(1,0)和点B(﹣3,0),与y轴交于点C,且OC=OB.

(1)求此抛物线的解析式;
(2)若点E为第二象限抛物线上一动点,连接BE,CE,求四边形BOCE面积的最大值,并求出此时点E的坐标;
(3)点P在抛物线的对称轴上,若线段PA绕点P逆时针旋转90°后,点A的对应点A′恰好也落在此抛物线上,求点P的坐标.
(4)连接AC,H是抛物线上一动点,过点H作AC的平行线交x轴于点F.是否存在这样的点F,使得以A,C,H,F为顶点所组成的四边形是平行四边形?若存在,求出满足条件的点F的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出
 关于
关于 轴对称的
轴对称的 .
.(2)写出点
 的坐标(直接写答案).
的坐标(直接写答案).A1_____________,B1______________,C1______________
-
科目: 来源: 题型:
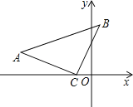
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90°,AC=BC,C点坐标为(﹣3,0),A点坐标为(﹣8,4),则B点的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC,BC=2AD,点F、G分别是边BC、CD的中点,连接AF、FG,过点D作DE∥FG交AF于点E.
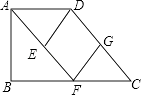
(1)求证:△AED≌△CGF;
(2)若梯形ABCD为直角梯形,∠B=90°,判断四边形DEFG是什么特殊四边形?并证明你的结论;
(3)若梯形ABCD的面积为a(平方单位),则四边形DEFG的面积为(平方单位).(只写结果,不必说理) -
科目: 来源: 题型:
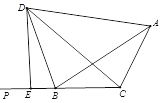
查看答案和解析>>【题目】如图,BD是△ABC的外角∠ABP的角平分线,DA=DC,DE⊥BP于点E,若AB=5,BC=3,则BE的长为 _____________
-
科目: 来源: 题型:
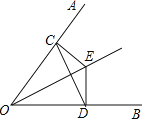
查看答案和解析>>【题目】如图,已知E是∠AOB的平分线上的一点,EC⊥OA,ED⊥OB,垂足分别是C,D.求证:OE垂直平分CD.
相关试题

