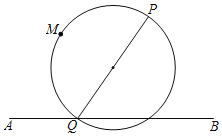
【题目】如图,平面上存在点P、点M与线段AB.若线段AB上存在一点Q,使得点M在以PQ为直径的圆上,则称点M为点P与线段AB的共圆点.
已知点P(0,1),点A(﹣2,﹣1),点B(2,﹣1).
(1)在点O(0,0),C(﹣2,1),D(3,0)中,可以成为点P与线段AB的共圆点的是 ;
(2)点K为x轴上一点,若点K为点P与线段AB的共圆点,请求出点K横坐标xK的取值范围;
(3)已知点M(m,﹣1),若直线y=![]() x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
x+3上存在点P与线段AM的共圆点,请直接写出m的取值范围.
参考答案:
【答案】(1)C;(2)﹣1﹣![]() ≤xk≤1﹣
≤xk≤1﹣![]() 或
或![]() ﹣1≤xk≤1+
﹣1≤xk≤1+![]() ;(3)m≤3﹣2
;(3)m≤3﹣2![]() 或m≥3+2
或m≥3+2![]() .
.
【解析】
(1)由题意可知当Q与A重合时,点C在以AP为直径的圆上,所以可以成为点P与线段AB的共圆点的是C;
(2)根据题意由两点的距离公式可得AP=BP=2![]() ,分别画以AP和BP为直径的圆交x轴于4个点:K1、K2、K3、K4,结合图形2可得4个点的坐标,从而得结论;
,分别画以AP和BP为直径的圆交x轴于4个点:K1、K2、K3、K4,结合图形2可得4个点的坐标,从而得结论;
(3)由题意先根据直线y=![]() x+3,当x=0和y=0计算与x轴和y轴的交点坐标,分两种情况:M在A的左侧和右侧,先计算圆E与直线y=
x+3,当x=0和y=0计算与x轴和y轴的交点坐标,分两种情况:M在A的左侧和右侧,先计算圆E与直线y=![]() x+3相切时m的值,从而根据图形可得结论.
x+3相切时m的值,从而根据图形可得结论.
解:(1)如图1,可以成为点P与线段AB的共圆点的是C,

故答案为:C;
(2)∵P(0,1),点A(﹣2,﹣1),点B(2,﹣1).
∴AP=BP=![]() =2
=2![]() ,
,
如图2,分别以PA、PB为直径作圆,交x轴于点K1、K2、K3、K4,

∵OP=OG=1,OE∥AB,
∴PE=AE=![]() ,
,
∴OE=![]() AG=1,
AG=1,
∴K1(﹣1﹣![]() ,0),k2(1﹣
,0),k2(1﹣![]() ,0),k3(
,0),k3(![]() ﹣1,0),k4(1+
﹣1,0),k4(1+![]() ,0),
,0),
∵点K为点P与线段AB的共圆点,
∴﹣1﹣![]() ≤xk≤1﹣
≤xk≤1﹣![]() 或
或![]() ﹣1≤xk≤1+
﹣1≤xk≤1+![]() ;
;
(3)分两种情况:
①如图3,当M在点A的左侧时,Q为线段AM上一动点,以PQ为直径的圆E与直线y=![]() x+3相切于点F,连接EF,则EF⊥FH,
x+3相切于点F,连接EF,则EF⊥FH,

当x=0时,y=3,当y=0时,y=![]() x+3=0,x=﹣6,
x+3=0,x=﹣6,
∴ON=3,OH=6,
∵tan∠EHF=![]() =
=![]() =
=![]() ,
,
设EF=a,则FH=2a,EH=![]() a,
a,
∴OE=6﹣![]() a,
a,
Rt△OEP中,OP=1,EP=a,
由勾股定理得:EP2=OP2+OE2,
∴![]() ,
,
解得:a=![]() (舍去)或
(舍去)或![]() ,
,
∴QG=2OE=2(6﹣![]() a)=﹣3+2
a)=﹣3+2![]() ,
,
∴m≤3﹣2![]() ;
;
②如图4,当M在点A的右侧时,Q为线段AM上一动点,以PQ为直径的圆E与直线y=![]() x+3相切于点F,连接EF,则EF⊥FH,
x+3相切于点F,连接EF,则EF⊥FH,
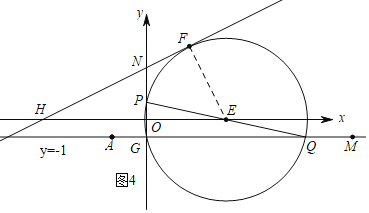
同理得QG=3+2![]() ,
,
∴m≥3+2![]() ,
,
综上,m的取值范围是m≤3﹣2![]() 或m≥3+2
或m≥3+2![]() .
.
-
科目: 来源: 题型:
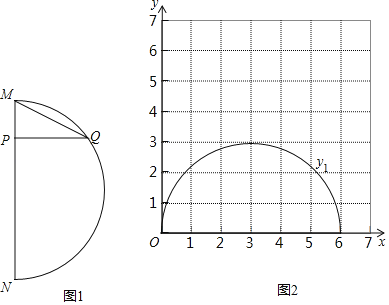
查看答案和解析>>【题目】如图1,在弧MN和弦MN所组成的图形中,P是弦MN上一动点,过点P作弦MN的垂线,交弧MN于点Q,连接MQ.已知MN=6cm,设M、P两点间的距离为xcm,P、Q两点间的距离为y1cm,M、Q两点间的距离为y2cm.小轩根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小轩的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值:x/cm.
x/cm
0
1
2
3
4
5
6
y1/cm
0
2.24
2.83
3.00
2.83
2.24
0
y2/cm
0
2.45
3.46
4.24
m
5.48
6
上表中m的值为 .(保留两位小数)
(2)在同一平面直角坐标系xOy(图2)中,函数y1的图象如图,请你描出补全后的表中y2各组数值所对应的点(x,y2),并画出函数y2的图象;
(3)结合函数图象,解决问题:当△MPQ有一个角是30°时,MP的长度约为 cm.(保留两位小数)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知抛物线y=ax2+bx﹣1交y轴于点P.
(1)过点P作与x轴平行的直线,交抛物线于点Q,PQ=4,求
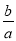 的值;
的值;(2)横纵坐标都是整数的点叫做整点.在(1)的条件下,记抛物线与x轴所围成的封闭区域(不含边界)为W.若区域W内恰有4个整点,结合函数图象,求a的取值范围.
-
科目: 来源: 题型:
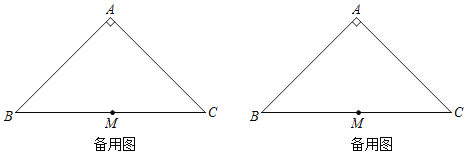
查看答案和解析>>【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,AB=AC=2,点M为BC中点.点P为AB边上一动点,点D为BC边上一动点,连接DP,以点P为旋转中心,将线段PD逆时针旋转90°,得到线段PE,连接EC.
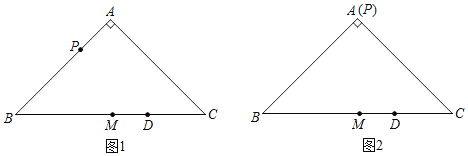
(1)当点P与点A重合时,如图2.
①根据题意在图2中完成作图;
②判断EC与BC的位置关系并证明.
(2)连接EM,写出一个BP的值,使得对于任意的点D总有EM=EC,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在⊙O中按如下步骤作图:
(1)作⊙O的直径AD;
(2)以点D为圆心,DO长为半径画弧,交⊙O于B,C两点;
(3)连接DB,DC,AB,AC,BC.
根据以上作图过程及所作图形,下列四个结论中错误的是( )
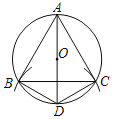
A.∠ABD=90°B.∠BAD=∠CBDC.AD⊥BCD.AC=2CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区响应国家提出的垃圾分类的号召,将生活垃圾分为厨余垃圾、可回收物、有害垃圾和其他垃圾四类,并分别设置了相应的垃圾箱.为了解居民生活垃圾分类的情况,随机对该区四类垃圾箱中总计1000吨生活垃圾进行分拣后,统计数据如表:
垃圾箱种类
垃圾量
垃圾种类(吨)
“厨余垃圾”箱
“可回收物”箱
“有害垃圾”箱
“其他垃圾”箱
厨余垃圾
400
100
40
60
可回收物
30
140
10
20
有害垃圾
5
20
60
15
其他垃圾
25
15
20
40

下列三种说法:
(1)厨余垃圾投放错误的有400t;
(2)估计可回收物投放正确的概率约为
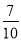 ;
;(3)数据显示四类垃圾箱中都存在各类垃圾混放的现象,因此应该继续对居民进行生活垃圾分类的科普.其中正确的个数是( )
A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,一次函数y=x+4的图象与y轴交于点A,与反比例函数y=
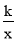 的图象的一个交点为M.
的图象的一个交点为M.(1)求点A的坐标;
(2)连接OM,如果△MOA的面积等于2,求k的值.
相关试题

