【题目】已知关于m的方程![]() (m-16)=7的解也是关于x的方程2(x-3)-n=52的解.
(m-16)=7的解也是关于x的方程2(x-3)-n=52的解.
(1)求m,n的值;
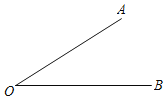
(2)已知∠AOB=m°,在平面内画一条射线OP,恰好使得∠AOP=n∠BOP,求∠BOP.
参考答案:
【答案】(1)m=30,n=2(2)30°或10°
【解析】
(1)先求出方程![]() (m-16)=7的解,然后把m的值代入方程2(x-3)-n=52,求出n的值;
(m-16)=7的解,然后把m的值代入方程2(x-3)-n=52,求出n的值;
(2)把m和n代入,然后根据OP的不同位置,即可算出∠BOP.
(1)∵![]() (m-16)=7,∴m=30,
(m-16)=7,∴m=30,
∵关于m的方程的![]() (m-16)=7解也是关于x的方程2(x-3)-n=52的解.
(m-16)=7解也是关于x的方程2(x-3)-n=52的解.
∴x=m,
将m=30,代入方程2(x-3)-n=52得:2(30-3)-n=52,
解得:n=2,
故m=30,n=2;
(2)∠AOB=30°,∠AOP=2∠BOP,
当OP在OB下方时如图,
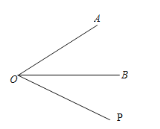
∵∠AOP=2∠BOP,∠AOP=∠AOB+∠BOP,
∴∠BOP=∠AOB
∵∠AOB=30°,
∴∠BOP=30°
当OP在OB和OA之间时如图,∠AOP=2∠BOP,∠BOP=10°
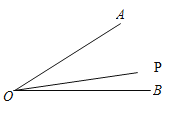
∵∠AOP=2∠BOP,∠AOP=∠AOB-∠BOP,
∴∠AOB=3∠BOP
∵∠AOB=30°,
∴∠BOP=10°
-
科目: 来源: 题型:
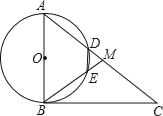
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.连结DE,使四边形DEBA为⊙O的内接四边形.
(1)求证:∠A=∠ABM=∠MDE;
(2)若AB=6,当AD=2DM时,求DE的长度;
(3)连接OD,OE,当∠A的度数为60°时,求证:四边形ODME是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=
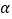 ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体
 ,如图所示.
,如图所示.
(1)请画出这个几何体
 的三视图.
的三视图.(2)若将此几何体
 的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.(3)若现在你的手头还有一些相同的小正方体可添放在几何体
 上,要保持主视图和左视图不变,则最多可以添加________个小正方体.
上,要保持主视图和左视图不变,则最多可以添加________个小正方体. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着出行方式的多样化,某地区打车有三种乘车方式,收费标准如下(假设打车的平均车速为30千米/小时):
网约出租车
网约顺风车
网约专车
3千米以内:12元
1.5元/千米
2元/千米
超过3千米的部分:2.4元/千米
0.5元/分钟
0.6元/分钟
(如:乘坐6千米,耗时12分钟,网约出租车的收费为:12+2.4×(6-3)=19.2(元);网约顺风车的收费为:6×1.5+12×0.5=15(元);网约专车的收费为:6×2+12×0.6=19.2(元))
请据此信息解决如下问题:
(1)王老师乘车从纵棹园去汽车站,全程8千米,如果王老师乘坐网约出租车,需要支付的打车费用为______元;
(2)李校长乘车从纵掉园去生态园,乘坐网约顺风车比乘坐网约出租车节省了2元.求从纵棹园去生态园的路程;
(3)网约专车为了和网约顺风车竞争客户,分别推出了优惠方式:网约顺风车对于乘车路程在5千米以上(含5千米)的客户每次收费立减6元;网约专车打车车费一律七五折优惠.对采用哪一种打车方式更合算提出你的建议.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣
 x2+
x2+ x+3
x+3 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).(1)求直线BC的函数表达式;
(2)①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.问:
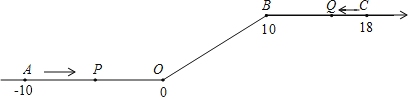
(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
相关试题

