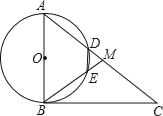
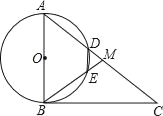
【题目】如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.连结DE,使四边形DEBA为⊙O的内接四边形.
(1)求证:∠A=∠ABM=∠MDE;
(2)若AB=6,当AD=2DM时,求DE的长度;
(3)连接OD,OE,当∠A的度数为60°时,求证:四边形ODME是菱形.
参考答案:
【答案】(1)证明见解析;(2)2;(3)证明见解析
【解析】试题分析:
(1)由∠ABC=90°及M是AC的中点可得AM=CM=BM,从而可得∠A=∠ABM,由四边形DEBA为⊙O的内接四边形可得∠ABM=∠MDE,由此即可得到∠A=∠ABM=∠MDE;
(2) 由(1)中结论可得DE∥AB,由此可得∴△MDE∽△MAB,从而可得![]() 结合AD=2DM及AB=6即可解得DE=2;
结合AD=2DM及AB=6即可解得DE=2;
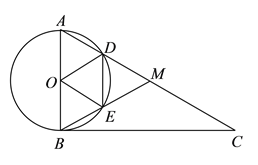
(3)如下图,由(1)中结论和∠A=60°易得∠AMB=60°,结合OA=OD=OE=OB可得△AOD、△OBE都是等边三角形,由此可得∠ADO=∠AMB=∠OEB=60°,由此可得OD∥BM,AM∥OE,这样即可得到四边形ODME是平行四边形,再结合OD=OE即可得到四边形ODME是菱形.
试题解析:
(1)∵∠ABC=90°,点M是AC的中点,
∴AM=CM=BM.
∴∠A=∠ABM.
∵四边形DEBA为⊙O的内接四边形,
∴∠ABM=∠MDE,
∴∠A=∠ABM=∠MDE.
(2)由(1)知∠A=∠ABM=∠MDE,
∴DE∥AB
∴△MDE∽△MAB
∴![]() ,
,
∵AD=2DM,
∴AM=3DM
∴![]() ,
,
∴DE=2.
(3)由(1)知∠A=∠ABM=∠MDE,
∵∠A=60°,
∴∠A=∠ABM=∠MDE=60°
∴∠AMB=60°
又∵OA=OD=OE=OB
∴△AOD、△OBE都是等边三角形
∴∠ADO=∠AMB=∠OEB=60°,
∴OD∥BM,AM∥OE
∴四边形ODME是平行四边形,
又∵OD=OE
∴四边形ODME是菱形
-
科目: 来源: 题型:
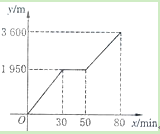
查看答案和解析>>【题目】小颖和小亮上山游玩,小颖乘坐缆车,小亮步行,两人相约在山顶的缆车终点会合.已知小亮行走到缆车终点的路程是缆车到山顶的线路长的2倍.小颖在小亮出发后50min 才乘上缆车,缆车的平均速度为180m/min.设小亮出发x min后行走的路程为y m,图中 的折线表示小亮在整个行走过程中y与x的函数关系.
(1)小亮行走的总路程是___________m,他途中休息了_____________min;
(2)①当50<x<80时,求y与x的函数关系式;②当小颖到达缆车终点时,小亮离缆车终点的路程是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD中,点M、N分别在AD,BC上,且AM=CN,MN与AC交于点O,连接DO,若∠BAC=28°,则∠ODC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,射线OC在∠A0B的内部,图中共有3个角:∠AOB、∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“定分线”
(1)一个角的平分线______这个角的“定分线”;(填“是”或“不是”)
(2)如图2,若∠MPN=
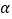 ,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)
,且射线PQ是∠MPN的“定分线”,则∠MPQ=_____(用含a的代数式表示出所有可能的结果)(3)如图2,若∠MPN=45°,且射线PQ绕点P从PN位置开始,以每秒10°的速度逆时针旋转,当PQ与PN成90°时停止旋转,旋转的时间为t秒.同时射线PM绕点P以每秒5°的速度逆时针旋转,并与PQ同时停止.当PQ是∠MPN的“定分线”时,求t的值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在桌面上,有若干个完全相同的小正方体堆成的一个几何体
 ,如图所示.
,如图所示.
(1)请画出这个几何体
 的三视图.
的三视图.(2)若将此几何体
 的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.
的表面喷上红漆(放在桌面上的一面不喷),则三个面上是红色的小正方体有_______个.(3)若现在你的手头还有一些相同的小正方体可添放在几何体
 上,要保持主视图和左视图不变,则最多可以添加________个小正方体.
上,要保持主视图和左视图不变,则最多可以添加________个小正方体. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于m的方程
 (m-16)=7的解也是关于x的方程2(x-3)-n=52的解.
(m-16)=7的解也是关于x的方程2(x-3)-n=52的解.(1)求m,n的值;
(2)已知∠AOB=m°,在平面内画一条射线OP,恰好使得∠AOP=n∠BOP,求∠BOP.
相关试题

