【题目】正方形的A1B1P1P2顶点P1、P2在反比例函数y= ![]() (x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y=
(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,再在其右侧作正方形P2P3A2B2 , 顶点P3在反比例函数y= ![]() (x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 .
(x>0)的图象上,顶点A2在x轴的正半轴上,则点P3的坐标为 . 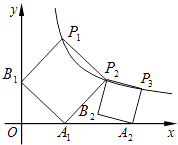
参考答案:
【答案】( ![]() +1,
+1, ![]() ﹣1)
﹣1)
【解析】解:作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,如图,
设P1(a, ![]() ),则CP1=a,OC=
),则CP1=a,OC= ![]() ,
,
∵四边形A1B1P1P2为正方形,
∴Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,
∴OB1=P1C=A1D=a,
∴OA1=B1C=P2D= ![]() ﹣a,
﹣a,
∴OD=a+ ![]() ﹣a=
﹣a= ![]() ,
,
∴P2的坐标为( ![]() ,
, ![]() ﹣a),
﹣a),
把P2的坐标代入y= ![]() (x>0),得到(
(x>0),得到( ![]() ﹣a)
﹣a) ![]() =2,解得a=﹣1(舍)或a=1,
=2,解得a=﹣1(舍)或a=1,
∴P2(2,1),
设P3的坐标为(b, ![]() ),
),
又∵四边形P2P3A2B2为正方形,
∴Rt△P2P3F≌Rt△A2P3E,
∴P3E=P3F=DE= ![]() ,
,
∴OE=OD+DE=2+ ![]() ,
,
∴2+ ![]() =b,解得b=1﹣
=b,解得b=1﹣ ![]() (舍),b=1+
(舍),b=1+ ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ﹣1,
﹣1,
∴点P3的坐标为 ( ![]() +1,
+1, ![]() ﹣1).
﹣1).
故答案为:( ![]() +1,
+1, ![]() ﹣1).
﹣1).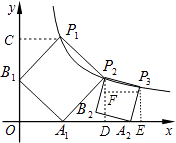
作P1C⊥y轴于C,P2D⊥x轴于D,P3E⊥x轴于E,P3F⊥P2D于F,设P1(a, ![]() ),则CP1=a,OC=
),则CP1=a,OC= ![]() ,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D=
,易得Rt△P1B1C≌Rt△B1A1O≌Rt△A1P2D,则OB1=P1C=A1D=a,所以OA1=B1C=P2D= ![]() ﹣a,则P2的坐标为(
﹣a,则P2的坐标为( ![]() ,
, ![]() ﹣a),然后把P2的坐标代入反比例函数y=
﹣a),然后把P2的坐标代入反比例函数y= ![]() ,得到a的方程,解方程求出a,得到P2的坐标;设P3的坐标为(b,
,得到a的方程,解方程求出a,得到P2的坐标;设P3的坐标为(b, ![]() ),易得Rt△P2P3F≌Rt△A2P3E,则P3E=P3F=DE=
),易得Rt△P2P3F≌Rt△A2P3E,则P3E=P3F=DE= ![]() ,通过OE=OD+DE=2+
,通过OE=OD+DE=2+ ![]() =b,这样得到关于b的方程,解方程求出b,得到P3的坐标.
=b,这样得到关于b的方程,解方程求出b,得到P3的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm,宽为n cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.则图②中两块阴影部分的周长和是( )cm.
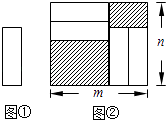
A.4m
B.4n
C.2(m+n)
D.4(m﹣n) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC= .
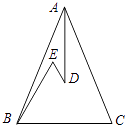
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小亮在学习探索三角形全等时,碰到如下一题:如图①,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系?

(1)请你帮他们解答,并说明理由;
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE,DE,则有CE=DE,你知道为什么吗(如图②)?
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有(2)中类似的结论.请你帮他在图③中画出图形,并写出结论,不要求说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△OAB与△OCD都是等边三角形,连接AC、BD相交于点E.
(1)求证:①△OAC≌△OBD,②∠AEB=60°;
(2)连结OE,OE是否平分∠AED?请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小李制作了一张△ABC纸片,点D、E分别在边AB、AC上,现将△ABC沿着DE折叠压平,使点A落在点A′位置.若∠A=75°,则∠1+∠2= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】图①表示的是某综合商场今年1~5月的商品各月销售总额的情况,图②表示的是商场服装部各月销售额占商场当月销售总额的百分比情况,观察图①、图②,解答下列问题:
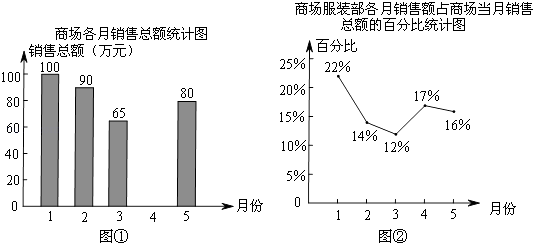
(1)来自商场财务部的数据报告表明,商场1~5月的商品销售总额一共是410万元,请你根据这一信息将图①中的统计图补充完整;
(2)商场服装部5月份的销售额是多少万元?
(3)小刚观察图②后认为,5月份商场服装部的销售额比4月份减少了.你同意他的看法吗?请说明理由.
相关试题

