【题目】已知:如图,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,过点
上一点,过点![]() 作
作![]() (垂足为
(垂足为![]() )交
)交![]() 于点
于点![]() ,且
,且![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() 交
交![]() 于点
于点![]()
![]() 求证:斜边
求证:斜边![]() 是
是![]() 的切线;
的切线;
![]() 设
设![]() 与
与![]() 相切的切点为
相切的切点为![]() ,
,![]() ,
,![]() ,连
,连![]() 、
、![]() ,求
,求![]() 的长.
的长.

参考答案:
【答案】(1)证明见解析; (2)![]() .
.
【解析】
(1)过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,可证明四边形FMCE是矩形,由EF//AC可知∠A=∠GFE,即可证明
,可证明四边形FMCE是矩形,由EF//AC可知∠A=∠GFE,即可证明![]() ,从而证明EG⊥AB,FM==EG,根据FM=CE可知EG=EC即可证明AB是
,从而证明EG⊥AB,FM==EG,根据FM=CE可知EG=EC即可证明AB是![]() 的切线;(2)由∠ACB=90°可知AC是切线,所以AG=AC,由EF=AF可求出FG的长,根据勾股定理可求出EG的长,根据勾股定理求出AE的长即可.
的切线;(2)由∠ACB=90°可知AC是切线,所以AG=AC,由EF=AF可求出FG的长,根据勾股定理可求出EG的长,根据勾股定理求出AE的长即可.
![]() 过
过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中

∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴斜边![]() 是
是![]() 的切线;
的切线;

![]() ∵
∵![]() ,
,
∴![]() 是
是![]() 的切线,
的切线,
∵![]() 是
是![]() 的切线,
的切线,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
即![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,由勾股定理得:
,由勾股定理得:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:
 内接于
内接于 ,过点
,过点 作直线
作直线 ,
, 为非直径的弦,且
为非直径的弦,且 是
是 的切线
的切线 求证:
求证: ;
; 若
若 ,
,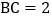 ,连接
,连接 并延长交
并延长交 于点
于点 ,求由弧
,求由弧 、线段
、线段 和
和 所围成的图形的面积.
所围成的图形的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
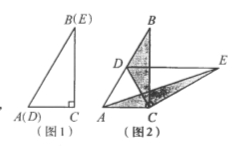


(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
-
科目: 来源: 题型:
查看答案和解析>>【题目】建立模型:
如图1,等腰Rt△ABC中,∠ABC=90°,CB=BA,直线ED经过点B,过A作AD⊥ED于D,过C作CE⊥ED于E.则易证△ADB≌△BEC.这个模型我们称之为“一线三垂直”.它可以把倾斜的线段AB和直角∠ABC转化为横平竖直的线段和直角,所以在平面直角坐标系中被大量使用.

模型应用:
(1)如图2,点A(0,4),点B(3,0),△ABC是等腰直角三角形.
①若∠ABC=90°,且点C在第一象限,求点C的坐标;
②若AB为直角边,求点C的坐标;
(2)如图3,长方形MFNO,O为坐标原点,F的坐标为(8,6),M、N分别在坐标轴上,P是线段NF上动点,设PN=n,已知点G在第一象限,且是直线y=2x一6上的一点,若△MPG是以G为直角顶点的等腰直角三角形,请直接写出点G的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选2名同学打第一场比赛,求下列事件的概率。
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在长方形OABC的边OA上,连接BP,过点P作BP的垂线,交射线OC于点Q,在点P从点A出发沿AO方向运动到点O的过程中,设AP=x,OQ=y,则下列说法正确的是( )

A.y随x的增大而增大B.y随x的增大而减小
C.随x的增大,y先增大后减小D.随x的增大,y先减小后增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】从一副扑克牌中取出方块3、红心6、黑桃10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字,这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同时,则视为平局.
(1)用画树状图或列表法,表示出小明、小丽两人一次游戏的所有可能的结果;
(2)求小明获胜的概率.
相关试题

