【题目】已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)若正方形ABCD的面积16,CF=3,求BE的长.

参考答案:
【答案】(1)详见解析;(2)5.
【解析】
(1)由正方形的性质得出BC=DC,∠BCE=∠DCF=90°,由SAS证明△BCE≌△DCF即可;
(2)由正方形的面积可求出边长BC的长,再利用勾股定理即可求出BE的长.
解:(1)证明:∵四边形ABCD是正方形,
∴BC=DC,∠BCE=90°,
∴∠DCF=90°,
在△BCE和△DCF中,
 ,
,
∴△BCE≌△DCF(SAS);
(2)∵正方形ABCD的面积16,
∴BC=4,
∵CF=3,
∴BE=![]() =5.
=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=8,AD=7.点P是长方形内一动点,点Q是DC边上的动点.若△ABP的面积为12,则AP+BP+PQ的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,下列说法不正确的是( )

A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC⊥BD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形 -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,AE⊥BC , AF⊥CD , 且E , F分别为BC , CD的中点,求∠EAF .

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:﹣12+(π﹣3.14)0﹣(﹣
 )﹣2+
)﹣2+ ;
;(2)先化简,再求值:[(2x+y)(2x﹣y)+(x+y)2﹣2(2x2﹣xy)]÷(﹣
 x),其中x、y满足
x),其中x、y满足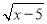 +(y+4)2=0.
+(y+4)2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,回答问题
在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(1)△CDF与△DEA是否相似?说明理由;
(2)求CF的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算: ÷
÷  ;
;
(2)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.
相关试题

