【题目】阅读材料,回答问题
在边长为1的正方形ABCD中,E是AB的中点,CF⊥DE,F为垂足.
(1)△CDF与△DEA是否相似?说明理由;
(2)求CF的长.
参考答案:
【答案】
(1)解:△ADE∽△FCD,理由如下:
∵四边形ABCD是正方形,
∴∠A=90°,AB∥CD,
∴∠CDF=∠DEA.
又CF⊥DE,
∴∠CFD=90°,即∠CFD=∠A,
因而,△ADE∽△FCD
(2)解:由题意知,AD=CD=1,AE= ![]() .
.
在直角△DEA中,有DE= ![]() =
= ![]() =
= ![]() .
.
由(1)可得: ![]() =
= ![]() ,则CF=
,则CF= ![]() =
= ![]()
【解析】(1)利用正方形的性质和平行线的性质,由两角法证明△ADE∽△FCD;
(2)根据勾股定理及相似三角形对应边成比例求解。
【考点精析】关于本题考查的勾股定理的概念和正方形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,AE⊥BC , AF⊥CD , 且E , F分别为BC , CD的中点,求∠EAF .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)若正方形ABCD的面积16,CF=3,求BE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:﹣12+(π﹣3.14)0﹣(﹣
 )﹣2+
)﹣2+ ;
;(2)先化简,再求值:[(2x+y)(2x﹣y)+(x+y)2﹣2(2x2﹣xy)]÷(﹣
 x),其中x、y满足
x),其中x、y满足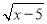 +(y+4)2=0.
+(y+4)2=0. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)计算: ÷
÷  ;
;
(2)如图,正方形ABCD中,点E,F,G分别在AB,BC,CD上,且∠EFG=90°.求证:△EBF∽△FCG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y=﹣
 x+b的图象与y轴交于点B(0,2),与反比例函数y=
x+b的图象与y轴交于点B(0,2),与反比例函数y= 的图象交于点A(4,﹣1).
的图象交于点A(4,﹣1).(1)求反比例函数的表达式和一次函数表达式;
(2)如果点P是x轴上的一点,且△ABP的面积是3,求P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是随机事件的是( )
A.任意选择某一电视频道,它正在播放新闻联播
B.三角形任意两边之和大于第三边
C. 是实数,
是实数, 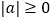
D.在一个装着白球和黑球的袋中摸球,摸出红球
相关试题

