【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() ﹣1来表示
﹣1来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:
∵22<(![]() )2<32,即2<
)2<32,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(![]() ﹣2).
﹣2).
请解答:
(1)![]() 的整数部分是 ,小数部分是
的整数部分是 ,小数部分是
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣![]() 的值.
的值.
参考答案:
【答案】(1)3, ![]() ﹣3;(2)4
﹣3;(2)4
【解析】(1)∵![]() <
<![]() <
<![]() ,
,

∴3<![]() <4,
<4,
∴![]() 的整数部分是3,小数部分是:
的整数部分是3,小数部分是:![]() ﹣3;
﹣3;
故答案为:3,![]() ﹣3;
﹣3;
(2)∵![]() <
<![]() <
<![]() ,
,
∴![]() 的小数部分为:a=
的小数部分为:a=![]() ﹣2,
﹣2,
∵![]() <
<![]() <
<![]() ,
,
∴![]() 的整数部分为b=6,
的整数部分为b=6,
∴a+b﹣![]() =
=![]() ﹣2+6﹣
﹣2+6﹣![]() =4.
=4.
-
科目: 来源: 题型:
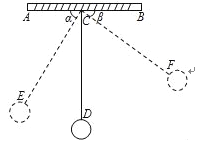
查看答案和解析>>【题目】如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面几何的学习过程中,我们经常会研究角和线之间的关系.
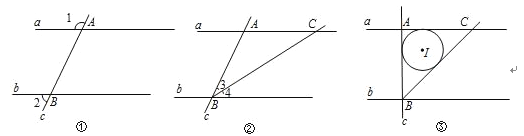
(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系 时,a∥b;
(2)如图②,在(1)中,作射线BC,与直线a的交点为C,当∠3、∠4满足何种数量关系时,AB=AC?证明你的结论;
(3)如图③,在(2)中,若∠BAC=90°,AB=2,⊙I为△ABC的内切圆.
①求⊙I的半径;
②P为直线a上一点,若⊙I上存在两个点M、N,使∠MPN=60°,直接写出AP长度的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(a﹣1,4)关于原点的对称点是点B(3,﹣2b﹣2),则a= ,b= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(-2x2y)3的结果是( )
A、-8x6y3 B、6x6y3 C、-8x5y3 D、-6x5y3
-
科目: 来源: 题型:
查看答案和解析>>【题目】三个底面为正方形,且高度相等的长方体容器甲、乙、丙,底面边长分别为5,12,13.今将甲、乙两个容器装满的水倒入丙容器中,则水是否会溢出?
相关试题

