【题目】在平面几何的学习过程中,我们经常会研究角和线之间的关系.
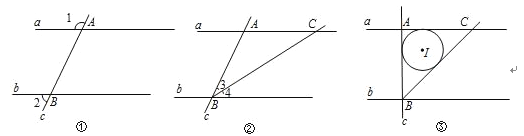
(1)如图①,直线a、b被直线c所截,交点分别为A、B.当∠1、∠2满足数量关系 时,a∥b;
(2)如图②,在(1)中,作射线BC,与直线a的交点为C,当∠3、∠4满足何种数量关系时,AB=AC?证明你的结论;
(3)如图③,在(2)中,若∠BAC=90°,AB=2,⊙I为△ABC的内切圆.
①求⊙I的半径;
②P为直线a上一点,若⊙I上存在两个点M、N,使∠MPN=60°,直接写出AP长度的取值范围.
参考答案:
【答案】(1)∠1+∠2=180°;(2)当∠3=∠4时,AB=AC;
(3)①![]() ;
;
②当点P在射线AC上时,0≤AP≤![]() ,
,
当点P在射线AC的反向延长线上时,0≤AP≤![]()
【解析】
试题分析:(1)根据平行线的性质和邻补角的定义即可得到结论;
(2)根据平行线的性质得到∠ACB=∠4,等量代换得到∠ACB=∠3,由等腰三角形的判定即可得到结论;
(3)①由(2)得AB=AC,推出△ABC是等腰直角三角形.根据勾股定理得到![]() ,由⊙I为△ABC的内切圆,得到四边形ADIF是正方形.根据切线长定理得到r=AD=
,由⊙I为△ABC的内切圆,得到四边形ADIF是正方形.根据切线长定理得到r=AD=![]() ,于是得到结论;
,于是得到结论;
②当点P在射线AC上时,得到0≤AP≤![]() ,当点P在射线AC的反向延长线上时,得到0≤AP≤
,当点P在射线AC的反向延长线上时,得到0≤AP≤![]() .
.
试题解析:(1)∠1+∠2=180°,
故答案为:∠1+∠2=180°;
(2)当∠3=∠4时,AB=AC,
证明:∵a∥b,
∴∠ACB=∠4,
又∵∠3=∠4,
∴∠ACB=∠3,
∴AB=AC;
(3)①由(2)得AB=AC,
又∵∠BAC=90°,
∴△ABC是等腰直角三角形.
∵AB=2,
∴AC=2.
∴在Rt△ABC中,![]() .
.
设D、E、F分别为边AB、BC、AC上的切点,
连接ID、IE、IF,
∵⊙I为△ABC的内切圆,
∴ID⊥AB、IE⊥BC、IF⊥AC.
∴AD=AF,BD=BE,CE=CF.
∵∠BAC=90°,
∴四边形ADIF是矩形.
∵ID=IF,
∴矩形ADIF是正方形.
∴r=AD=![]() .
.
∴⊙I的半径为![]() ;
;
②当点P在射线AC上时,0≤AP≤![]() ,
,
当点P在射线AC的反向延长线上时,0≤AP≤![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平阳中学长方形足球场的周长为310米,长比宽多25米,问这个足球场的长和宽分别是多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)将直角三角形ABC(∠C为直角)按如图1放置,使得坐标原点与点C重合,已知A(a,3),B(b,-3),且a+b=8,求三角形ACB的面积:
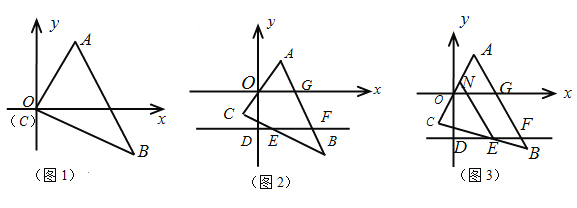
(2)将直角三角形ACB(∠C为直角)按如图2方式放置,使得点O在边AC上,D是y轴上一点,过D作DF//x轴,交AB于F点,AB交x轴于点G, BC交DF于点E, 若∠AOG=50°,求∠BEF的度数。
将直角三角形ACB(∠C为直角)按照如图3方式放置,使得∠C在x轴于DF之间,N为AC边上一点,且∠NEC+∠CEF=180°,写出∠NEF与∠AOG之间的数量关系,并证明你的结论。
-
科目: 来源: 题型:
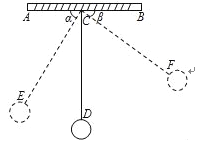
查看答案和解析>>【题目】如图,物理实验室有一单摆在左右摆动,摆动过程中选取了两个瞬时状态,从C处测得E、F两点的俯角分别为∠ACE=α,∠BCF=β,这时点F相对于点E升高了acm.求该摆绳CD的长度.(用含a、α、β的式子表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题:大家知道
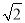 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此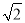 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用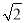 ﹣1来表示
﹣1来表示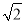 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为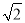 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<(
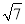 )2<32,即2<
)2<32,即2<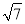 <3,∴
<3,∴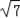 的整数部分为2,小数部分为(
的整数部分为2,小数部分为(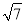 ﹣2).
﹣2).请解答:
(1)
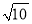 的整数部分是 ,小数部分是
的整数部分是 ,小数部分是 (2)如果
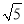 的小数部分为a,
的小数部分为a, 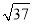 的整数部分为b,求a+b﹣
的整数部分为b,求a+b﹣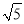 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(a﹣1,4)关于原点的对称点是点B(3,﹣2b﹣2),则a= ,b= .
相关试题

