【题目】如图,在△ABC中,以边AB上的一点O为圆心,以OA的长为半径的圆交边AB于点D,BC与⊙O相切于点C.若⊙O的半径为5,∠A=20°,则 ![]() 的长为 .
的长为 . 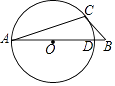
参考答案:
【答案】![]()
【解析】解:连接OC, 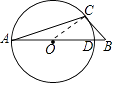
∵AO=CO,
∴∠A=∠ACO=20°,
∴∠COD=40°,
∴ ![]() 的长=
的长= ![]() =
= ![]() ,
,
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用切线的性质定理和弧长计算公式的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;若设⊙O半径为R,n°的圆心角所对的弧长为l,则l=nπr/180;注意:在应用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,从点
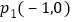




 ... 依次扩展下去,则
... 依次扩展下去,则  的坐标为 ( )
的坐标为 ( ) 
A. (505,-505)B. (-505,505)C. (-505,504)D. (-506,505)
-
科目: 来源: 题型:
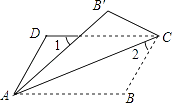
查看答案和解析>>【题目】如图,将ABCD沿对角线AC折叠,使点B落在点B'处.若∠1=∠2=44°,则∠B的大小为度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xoy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
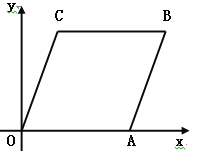
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中。

(1)请写出△ABC各点的坐标;
(2)求出△ABC的面积S△ABC;
(3)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
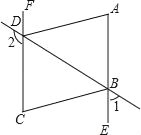
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
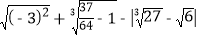
(2)如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,求∠GHC度数
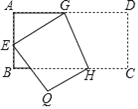
相关试题

