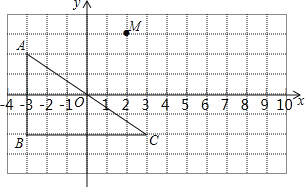
【题目】如图,已知Rt△ABC的三个顶点分别为A(-3,2),B(-3,-2),C(3,-2).将△ABC平移,使点A与点M(2,3)重合,得到△MNP.
(1)将△ABC向 平移 个单位长度,然后再向 平移 个单位长度,可以得到△MNP.
(2)画出△MNP.
(3)在(1)的平移过程中,线段AC扫过的面积为 (只需填入数值,不必写单位).
参考答案:
【答案】(1)右,5,上,1;(2)见解析;(3)26.
【解析】
(1)利用网格特点和平移的性质得出答案;
(2)再利用(1)中平移的性质得出△MNP;
(3)先由AC平移到A1C1,再由A1C1平移到MP,所以线段AC扫过的部分为两个平行四边形,于是根据平行四边形的面积公式可计算出线段AC扫过的面积.
解:(1)将△ABC向右平移5个单位长度,然后再向上平移1个单位长度,可以得到△MNP;
故答案为:右,5,上,1;
(2)如图所示:△MNP,即为所求;
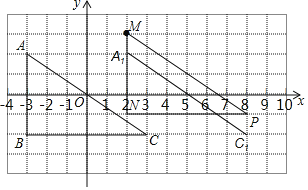
(3)线段AC扫过的面积为:4×5+1×6=26.
故答案为:26.
-
科目: 来源: 题型:
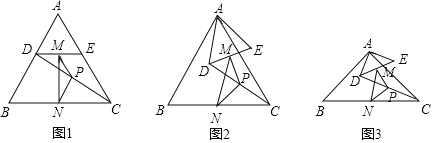
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,点D,E分别在边AB、AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
在如图中,线段PM与PN的数量关系是______,∠MPN的度数是______;
(2)探究证明
把△ADE绕点A逆时针方向旋转到如图的位置,
①判断△PMN的形状,并说明理由;
②求∠MPN的度数;
(3)拓展延伸
若△ABC为直角三角形,∠BAC=90°,AB=AC=12,点DE分别在边AB,AC上,AD=AE=4,连接DC,点M,P,N分别为DE,DC,BC的中点.把△ADE绕点A在平面内自由旋转,如图.
①△PMN的是______三角形.
②直接利用①中的结论,求△PMN面积的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,3)、B(4,2)、C(2,1).
(1)作出与△ABC关于x轴对称的△A 1B1C1,并写出点A1的坐标;
(2)以原点O 为位似中心,在原点的另一侧画出△A2B2C2,使
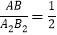 ,并写出点A2的坐标.
,并写出点A2的坐标.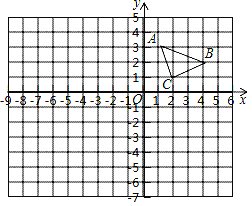
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求
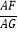 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,已知AD=12,AB=9,E是BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为_____.
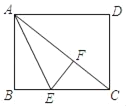
-
科目: 来源: 题型:
查看答案和解析>>【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:

(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
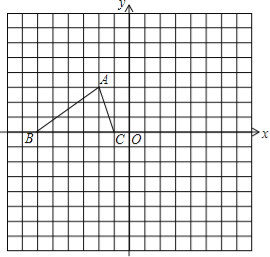
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
相关试题

