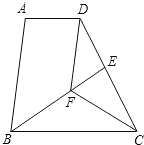
【题目】已知:如图,在梯形ABCD中,AD∥BC,BC=DC,CF平分∠BCD,DF∥AB,BF的延长线交DC于点E.求证:
(1)△BFC≌△DFC;
(2)AD=DE.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)由CF平分∠BCD可知∠BCF=∠DCF,然后通过SAS就能证出△BFC≌△DFC.
(2)要证明AD=DE,连接BD,证明△BAD≌△BED则可.AB∥DF∠ABD=∠BDF,又BF=DF∠DBF=∠BDF,∴∠ABD=∠EBD,BD=BD,再证明∠BDA=∠BDC则可,容易推理∠BDA=∠DBC=∠BDC.
试题解析:(1)∵CF平分∠BCD,
∴∠BCF=∠DCF.
在△BFC和△DFC中,
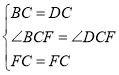
∴△BFC≌△DFC(SAS).
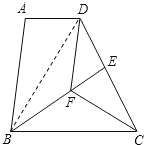
(2)连接BD.
∵△BFC≌△DFC,
∴BF=DF,∴∠FBD=∠FDB.
∵DF∥AB,
∴∠ABD=∠FDB.
∴∠ABD=∠FBD.
∵AD∥BC,
∴∠BDA=∠DBC.
∵BC=DC,
∴∠DBC=∠BDC.
∴∠BDA=∠BDC.
又∵BD是公共边,
∴△BAD≌△BED(ASA).
∴AD=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点A(-3,2)关于y轴对称点的坐标是( )
A.(3,2)
B.(2,3)
C.(-3,-2)
D.(-2,-3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果(x+1)(x+m)的乘积中不含x的一次项,则m的值为 ______ .
-
科目: 来源: 题型:
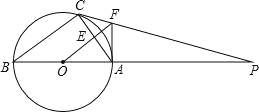
查看答案和解析>>【题目】如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC,交AC于点E,交PC于点F,连接AF.
(1)求证:AF是⊙O的切线;
(2)已知⊙O的半径为4,AF=3,求线段AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正多边形一个外角的度数是45°,则该正多边形的边数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成推理填空:如图在△ABC中,已知∠1+∠2=180°,∠3=∠B,试说明∠AED=∠C.
解:∵∠1+∠EFD=180°(邻补角定义),∠1+∠2=180°(已知 )
∴ (同角的补角相等)①
∴ (内错角相等,两直线平行)②
∴∠ADE=∠3( )③
∵∠3=∠B( )④
∴ (等量代换)⑤
∴DE∥BC( )⑥
∴∠AED=∠C( )⑦

-
科目: 来源: 题型:
查看答案和解析>>【题目】互为相反数的两数在数轴上的两点间的距离为11,这两个数为_______.
相关试题

