【题目】我市某中学计划购进若干个甲种规格的排球和乙种规格的足球. 如果购买20个甲种规格的排球和15个乙种规格的足球,一共需要花费2050元; 如果购买10个甲种规格的排球和20个乙种规格的足球,一共需要花费1900元.
(1)求每个甲种规格的排球和每个乙种规格的足球的价格分别是多少元?
(2)如果学校要购买甲种规格的排球和乙种规格的足球共50个,并且预算总费用不超过3210元,那么该学校至多能购买多少个乙种规格的足球?
参考答案:
【答案】(1)50,70;(2)35;
【解析】
(1)甲乙规格的球价格分别设为x,y,根据题意列出二元一次方程组,即可求出结果;
(2)设未知数x,根据题意以及一问中的结果列出不等式,解不等式,取整,即为所求答案.
(1)设每个甲种规格的排球的价格是x元,每个乙种规格的足球的价格是y元,
根据题意得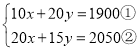 ,
,
解得:![]() ,
,
答:每个甲种规格的排球的价格是50元,每个乙种规格的足球的价格是70元;
(2)设该学校购买m个乙种规格的足球,则购买甲种规格的排球(50-m)个,根据题意得出:50(50-m)+70m≤3210,解得m≤35.5;
答:该学校至多能购买35个乙种规格的足球.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
(1)△ABC的面积为 ;
(2)将△ABC经过平移后得到△A′B′C′,图中标出了点B的对应点B',补全△A′B′C′;
(3)在图中画出△ABC的高CD;
(4)能使S△ABC=S△QBC的格点Q(A点除外)共有 个.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市投入1380元资金购进甲、乙两种矿泉水共50箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价(元/箱)
销售价(元/箱)
甲
24
36
乙
33
48
(1)该超市购进甲、乙两种矿泉水各多少箱?
(2)全部售完50箱矿泉水,该超市共获得利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l1的解析式为
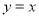 ,直线l2的解析式为
,直线l2的解析式为 ,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.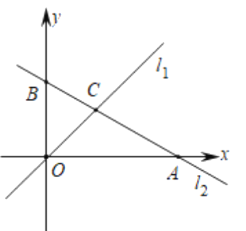

(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,请求出点P的坐标;
(3)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )

A. 24m B. 22m C. 20m D. 18m
-
科目: 来源: 题型:
查看答案和解析>>【题目】亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部
 , 颖颖的头顶
, 颖颖的头顶 及亮亮的眼睛
及亮亮的眼睛 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置 ,
,  . 然后测出两人之间的距离
. 然后测出两人之间的距离 , 颖颖与楼之间的距离
, 颖颖与楼之间的距离 (
( ,
,  ,
,  在一条直线上),颖颖的身高
在一条直线上),颖颖的身高 , 亮亮蹲地观测时眼睛到地面的距离
, 亮亮蹲地观测时眼睛到地面的距离 . 你能根据以上测量数据帮助他们求出住宅楼的高度吗?
. 你能根据以上测量数据帮助他们求出住宅楼的高度吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次向左跳动至A1(﹣1,1),第二次向右跳动至A2(2,1),第三次向左跳动至A3(﹣2,2),第四次向右跳动至A4(3,2)…依照此规律跳动下去,点A第124次跳动至A124的坐标( )

A.(63,62)B.(62,61)C.(﹣62,61)D.(124,123)
相关试题

