搜索
【题目】如图（1）所示为一上面无盖的正方体纸盒，现将其剪开展成平面图，如图（2）所示．已知展开图中每个正方形的边长为1．
（1）求在该展开图中可画出最长线段的长度？这样的线段可画几条？
（2）试比较立体图中
与平面展开图中
的大小关系？
参考答案：
【答案】（1）
，4条（2）相等
【解析】解：（1）在平面展开图中可画出最长的线段长为．
··········································1分
如图（1）中的
，在
中
，由勾股定理得：
··········································3分
答：这样的线段可画4条（另三条用虚线标出）．······4分
（2）
立体图中
为平面等腰直角三角形的一锐角，
．········································5分
在平面展开图中，连接线段
，由勾股定理可得：
．········································7分
又
，
由勾股定理的逆定理可得
为直角三角形．
又
，
为等腰直角三角形．···························8分
．········································9分
所以
与
相等．10分
（1）利用勾股定理求得在平面展开图中可画出最长的线段长为，由图可知这样的线段可画4条
（2）立体图中
为平面等腰直角三角形的一锐角，是
，在平面展开图中，连接线段，由勾股定理可得，
，由勾股定理的逆定理可得为直角三角形，又
，得
， 即可得出与相等
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司为了解员工对“六五”普法知识的知晓情况，从本公司随机选取40名员工进行普法知识考查，对考查成绩进行统计（成绩均为整数，满分100分），并依据统计数据绘制了如下尚不完整的统计表．解答下列问题：
组别
分数段/分
频数/人数
频率
1
50.5～60.5
2
a
2
60.5～70.5
6
0.15
3
70.5～80.5
b
c
4
80.5～90.5
12
0.30
5
90.5～100.5
6
0.15
合计
40
1.00
（1）表中a= ， b= ， c=；
（2）请补全频数分布直方图；
（3）该公司共有员工3000人，若考查成绩80分以上（不含80分）为优秀，试估计该公司员工“六五”普法知识知晓程度达到优秀的人数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了对一棵倾斜的古杉树AB进行保护，需测量其长度．如图，在地面上选取一点C，测得∠ACB=45°，AC=24m，∠BAC=66.5°，求这棵古杉树AB的长度．（结果取整数） 参考数据：
≈1.41，sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AC=BC，AB是⊙C的切线，切点为D，直线AC交⊙C于点E、F，且CF=
AC．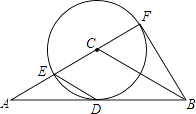 
（1）求∠ACB的度数；
（2）若AC=8，求△ABF的面积． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．下列结论：①△ABG≌△AFG；②BG=GC；③AG∥CF；④S△FGC=3．其中正确结论的个数是（ ）
-
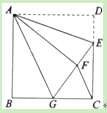
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A（1，6）和点M（m，n）都在反比例函数y=
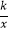（x＞0）的图象上，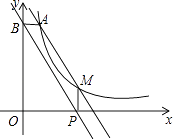
（1）k的值为；
（2）当m=3，求直线AM的解析式；
（3）当m＞1时，过点M作MP⊥x轴，垂足为P，过点A作AB⊥y轴，垂足为B，试判断直线BP与直线AM的位置关系，并说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，矩形OABC顶点B的坐标为（8，3），定点D的坐标为（12，0），动点P从点O出发，以每秒2个单位长度的速度沿x轴的正方向匀速运动，动点Q从点D出发，以每秒1个单位长度的速度沿x轴的负方向匀速运动，PQ两点同时运动，相遇时停止．在运动过程中，以PQ为斜边在x轴上方作等腰直角三角形PQR．设运动时间为t秒．
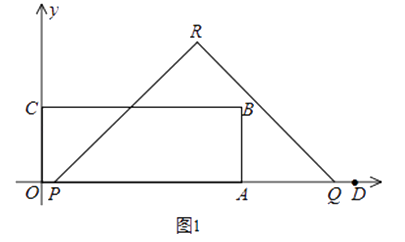
（1）当t=时，△PQR的边QR经过点B；
（2）设△PQR和矩形OABC重叠部分的面积为S，求S关于t的函数关系式；
（3）如图2，过定点E（5，0）作EF⊥BC，垂足为F，当△PQR的顶点R落在矩形OABC的内部时，过点R作x轴、y轴的平行线，分别交EF、BC于点M、N，若∠MAN=45°，求t的值．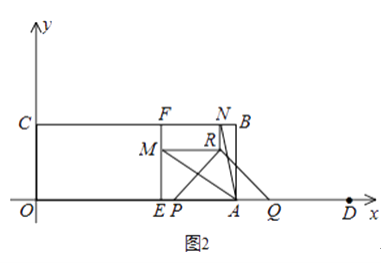
相关试题
