【题目】如图,点P、Q是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,连接AQ、CP交于点M,则在P、Q运动的过程中,下列结论错误的是( )

A.BP=CM
B.△ABQ≌△CAP
C.∠CMQ的度数不变,始终等于60°
D.当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形
秒时,△PBQ为直角三角形
参考答案:
【答案】A
【解析】
A、等边三角形ABC中,AB=BC,而AP=BQ,所以BP=CQ;
B、根据等边三角形的性质,利用SAS证明△ABQ≌△CAP;
C、由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠CMQ=60°;
D、设时间为t秒,则AP=BQ=tcm,PB=(4-t)cm,当∠PQB=90°时,因为∠B=60°,所以PB=2BQ,即4-t=2t故可得出t的值,当∠BPQ=90°时,同理可得BQ=2BP,即t=2(4-t),由此两种情况即可得出结论.
解:A、在等边△ABC中,AB=BC.
∵点P、Q的速度都为1cm/s,
∴AP=BQ,
∴BP=CQ.
只有当CM=CQ时,BP=CM.
故A错误;
B、∵△ABC是等边三角形
∴∠ABQ=∠CAP,AB=CA,
又∵点P、Q运动速度相同,
∴AP=BQ,
在△ABQ与△CAP中,
∵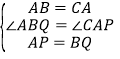 ,
,
∴△ABQ≌△CAP(SAS).
故B正确;
C、点P、Q在运动的过程中,∠QMC不变.
理由:∵△ABQ≌△CAP,
∴∠BAQ=∠ACP,
∵∠QMC=∠ACP+∠MAC,
∴∠CMQ=∠BAQ+∠MAC=∠BAC=60°.
故C正确;
D、设时间为t秒,则AP=BQ=tcm,PB=(4-t)cm,
当∠PQB=90°时,
∵∠B=60°,
∴PB=2BQ,即4-t=2t,t=![]() ,
,
当∠BPQ=90°时,
∵∠B=60°,
∴BQ=2BP,得t=2(4-t),t=![]() ,
,
∴当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.
秒时,△PBQ为直角三角形.
故D正确.故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)填表:
a
0.000 001
0.001
1
1 000
1 000 000

(2)由上表你发现了什么规律?请用语言叙述这个规律:______________________________.
(3)根据你发现的规律填空:
①已知
 =1.442,则
=1.442,则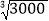 =__________,
=__________, =__________;
=__________;②已知
 =0.076 96,则
=0.076 96,则 =__________.
=__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是∠AOB外的一点,点M,N分别是∠AOB两边上的点,点P关于OA的对称点Q恰好落在线段MN上,点P关于OB的对称点R落在MN的延长线上.若PM=3cm,PN=4cm,MN=4.5cm,则线段QR的长为( )
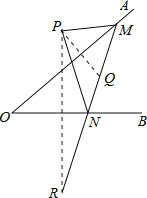
A.4.5 B.5.5 C.6.5 D.7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数
 图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1<y2;③2a﹣b=0;④
图象的一部分,图象过点A(-3,0),对称轴为直线x=﹣1,给出四个结论:①c>0;②若点B(-1.5,y1)、C(-2.5,y2)为函数图象上的两点,则y1<y2;③2a﹣b=0;④  <0.其中正确结论的个数是( )
<0.其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,AB=6,AN=2,∠BAC的平分线交BC于点D,M是AD上的动点,则BM+MN的最小值是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】仔细观察下面的日历,回答下列问题:
(1)任意用正方形框圈出四个日期,如果正方形框中的第一个数(左上角的数)为
 ,用代数式表示正方形框中的四个数的和;
,用代数式表示正方形框中的四个数的和;(2)若将正方形框上下左右移动,可框住另外的四个数,这四个数的和能等于
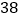 吗?如果能,依次写出这四个数;如果不能,请说明理由.
吗?如果能,依次写出这四个数;如果不能,请说明理由.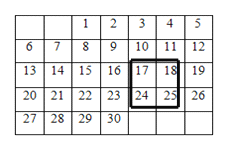
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列两个等式:
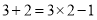 ,
,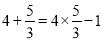 ,给出定义如下:我们称使等式
,给出定义如下:我们称使等式 成立的一对有理数
成立的一对有理数 为“理想有理数对”,记为
为“理想有理数对”,记为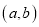 ,如:数对
,如:数对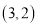 、
、 都是“理想有理数对”.
都是“理想有理数对”.(1)数对
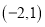 、
、 中是“理想有理数对”的是______;
中是“理想有理数对”的是______;(2)若
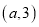 是“理想有理数对”,求a的值;
是“理想有理数对”,求a的值;(3)若
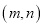 是“理想有理数对”,则
是“理想有理数对”,则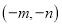 ______“理想有理数对”(填“是”、“不是”或“不确定”);
______“理想有理数对”(填“是”、“不是”或“不确定”);(4)请再写出一对符合条件的“理想有理数对”.(不能与题目中已有的数对重复).
相关试题

