【题目】下列条件:①∠A﹣∠B=∠C; ②∠A:∠B:∠C=2:3:5; ③∠A=![]() ∠B=
∠B= ![]() ∠ C;④∠A=∠B=2∠C;⑤∠A=∠B=
∠ C;④∠A=∠B=2∠C;⑤∠A=∠B= ![]() ∠C,其中能确定△ABC 为直角三角形的条件有 ( )
∠C,其中能确定△ABC 为直角三角形的条件有 ( )
A.2 个B.3 个C.4 个D.5 个
参考答案:
【答案】C
【解析】
根据三角形内角和定理、直角三角形的定义解答.
解:①∵∠A﹣∠B=∠C,
∴∠A=∠B+∠C,
∴∠A=90°,即△ABC为直角三角形;
②设∠A、∠B、∠C分别为2x、3x、5x,
由三角形内角和定理得,2x+3x+5x=180°,
解得,x=18°,
∠C=5x=90°,即△ABC为直角三角形;
③∠A=![]() ∠B=
∠B=![]() ∠C,
∠C,
则∠C=3∠A,∠B=2∠A,
由三角形内角和定理得,∠A+2∠A+3∠A=180°,
解得,∠A=30°,
∴∠C=3∠A=90°,即△ABC为直角三角形;
④∠A=∠B=2∠C,
由三角形内角和定理得,2∠C+2∠C+∠C=180°,
解得,∠C=36°,∠A=∠B=2∠C=72°,即△ABC不是直角三角形;
⑤∠A=∠B=![]() ∠C,
∠C,
由三角形内角和定理得,![]() ∠C+
∠C+![]() ∠C+∠C=180°,
∠C+∠C=180°,
解得,∠C=90°,即△ABC是直角三角形;
故选:C.
-
科目: 来源: 题型:
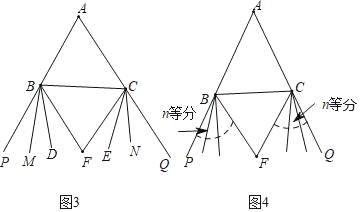
查看答案和解析>>【题目】(1)如图1,已知△ABC,BF平分外角∠CBP,CF平分外角∠BCQ.试确定∠A和∠F的数量关系;
(2)如图2,已知△ABC,BF和BD三等分外角∠CBP,CF和CE三等分外角∠BCQ.试确定∠A和∠F的数量关系;
(3)如图3,已知△ABC,BF、BD和BM四等分外角∠CBP,CF、CE和CN四等分外角∠BCQ.试确定∠A和∠F的数量关系;
(4)如图4,已知△ABC,将外角∠CBP进行n等分,BF是临近BC边的等分线,将外角∠BCQ进行n等分,CF是临近BC边的等分线,试确定∠A和∠F的数量关系.

-
科目: 来源: 题型:
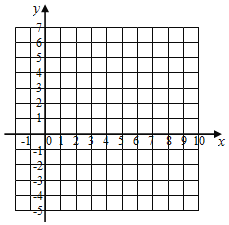
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(6,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2+
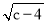 =0,
=0,(1)求A.B.C的坐标;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点P,使三角形APC的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=
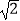 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 . 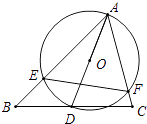
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在矩形ABCD中,BC=8,CD=6,将△BCD沿对角线BD翻折,点C落在点C′处,BC′交AD于点E,则△BDE的面积为( )

A.
 B.
B.  C. 21D. 24
C. 21D. 24 -
科目: 来源: 题型:
查看答案和解析>>【题目】在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.

(1)这50名同学捐款的众数为元,中位数为元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,AB=6,第1次平移将长方形ABCD沿AB的方向向右平移5个单位,得到长方形A1B1C1D1,第2次平移将长方形A1B1C1D1沿A1B1的方向向右平移5个单位,得到长方形A2B2C2D2,…,以此类推,第n次平移将长方形An﹣1Bn﹣1Cn﹣1Dn﹣1沿An﹣1Bn﹣1的方向向右平移5个单位,得到长方形AnBnCnDn(n>2),则ABn长为 ( )

A. 5n+6B. 5n+1C. 5n+4D. 5n+3
相关试题

