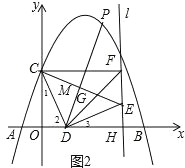
【题目】如图,抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0),交y轴于点C,点D是线段OB上一动点,连接CD,将CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴,垂足为H,过点C作CF⊥l于F,连接DF,CE交于点G.
(1)求抛物线解析式;
(2)求线段DF的长;
(3)当DG=![]() 时,
时,
①求tan∠CGD的值;
②试探究在x轴上方的抛物线上,是否存在点P,使∠EDP=45°?若存在,请写出点P的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)抛物线解析式为:y=﹣![]() x2+
x2+![]() x+3;(2)DF=
x+3;(2)DF=![]() =3
=3![]() ;(3)①tan∠CGD=3;
;(3)①tan∠CGD=3;
②P点坐标为(![]() ,
,![]() ).
).
【解析】
试题分析:(1)把A点和B点坐标代入y=ax2+bx+3中得到关于a、b的方程组,然后解方程组求出a、b即可得到抛物线解析式;
(2)如图1,先求出C点坐标,再根据旋转的性质得到CD=DE,∠CDE=90°,再证明△OCD≌△HDE得到HD=OC=3,接着说明四边形OCFH为矩形得到HF=OC=3,然后利用勾股定理计算DF;
(3)①利用△CDE和△DFH都是等腰直角三角形得到∠DCE=45°,∠DFH=45°,于是有∠DFC=45°,则可证明△DCG∽△DFC,根据相似的性质得![]() =
=![]() ,∠DGC=∠DCF,接着利用相似比可计算出CD=
,∠DGC=∠DCF,接着利用相似比可计算出CD=![]() ,利用∠DCF=∠2得到∠CGD=∠2,然后在Rt△OCD中求出∠2的正切值即可得到tan∠CGD的值;
,利用∠DCF=∠2得到∠CGD=∠2,然后在Rt△OCD中求出∠2的正切值即可得到tan∠CGD的值;
②根据△DCG∽△DFC得到HD=OC=3,EH=OD=1,则E(4,1),取CE的中点M,如图2,利用线段的中点坐标公式得到M(2,2),根据等腰直角三角形的性质判断DP经过CE的中点M,接下来利用待定系数法求出直线DP的解析式为y=2x﹣2,然后解方程组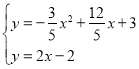 可得P点坐标.
可得P点坐标.
试题解析:(1)∵抛物线y=ax2+bx+3交x轴于A(﹣1,0)和B(5,0),
∴![]() ,解得
,解得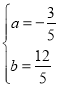 ,∴抛物线解析式为:y=﹣
,∴抛物线解析式为:y=﹣![]() x2+
x2+![]() x+3;
x+3;
(2)当x=0时,y=﹣![]() x2+
x2+![]() x+3=3,则C(0,3),如图1,
x+3=3,则C(0,3),如图1,
∵CD绕点D顺时针旋转90°得到线段DE,
∴CD=DE,∠CDE=90°,
∵∠2+∠3=90°,
而∠1+∠2=90°,
∴∠1=∠3,
在△OCD和△HDE中
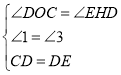 ,
,
∴△OCD≌△HDE,
∴HD=OC=3,
∵CF⊥BF,
∴四边形OCFH为矩形,
∴HF=OC=3,
∴DF=![]() =3
=3![]() ;
;
(3)①∵△CDE和△DFH都是等腰直角三角形,如图1,
∴∠DCE=45°,∠DFH=45°,
∴∠DFC=45°,
而∠CDG=∠FDC,
∴△DCG∽△DFC,
∴![]() ,∠DGC=∠DCF,即
,∠DGC=∠DCF,即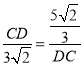 ,解得CD=
,解得CD=![]() ,
,
∵CF∥OH,
∴∠DCF=∠2,
∴∠CGD=∠2,
在Rt△OCD中,OD=![]() =
=![]() =1,
=1,
∴tan∠2=![]() =3,
=3,
∴tan∠CGD=3;
②∵OD=1,
∴D(1,0),
∵△OCD≌△HDE,
∴HD=OC=3,EH=OD=1,
∴E(4,1),
取CE的中点M,如图2,则M(2,2),
∵△DCE为等腰直角三角形,∠EDP=45°,
∴DP经过CE的中点M,
设直线DP的解析式为y=mx+n,
把D(1,0),M(2,2)代入得![]() ,解得
,解得![]() ,
,
∴直线DP的解析式为y=2x﹣2,
解方程组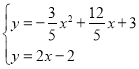 得
得 或
或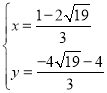 (舍去),
(舍去),
∴②P点坐标为(![]() ,
,![]() ).
).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
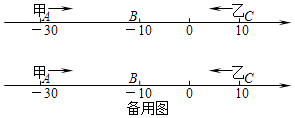
(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A,B,C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】北京故宫有着近六百年的历史,是最受中外游客喜爱的景点之一,其年接待量在2019年首次突破19000000人次大关.将19000000用科学记数法可表示为( )
A.0.19×108B.0.19×107C.1.9×107D.19×106
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法不正确的是( ).
A.所有的有理数都有相反数
B.正数与负数互为相反数
C.在一个数的前面添上“-”,就得到它的相反数.
D.在数轴上到原点距离相等的两个点所表示的数是互为相反数 -
科目: 来源: 题型:
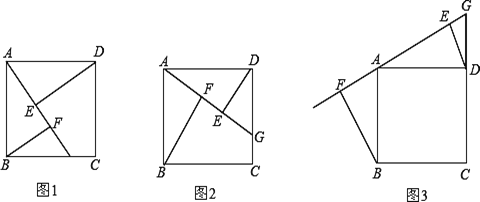
查看答案和解析>>【题目】四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)
如图1,点G是BC边上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E.求证:△ABF≌△DAE;
(2) ①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E,线段EF与AF、BF的等量关系是______ ___;
②如图3,若点G是CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,
线段EF与AF、BF的等量关系是______ ;
(3)若点G是BC延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,请画图并
探究线段EF与AF、BF的等量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2(x﹣1)+1=0;
(2) x﹣1=
x﹣1= 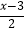 .
. -
科目: 来源: 题型:
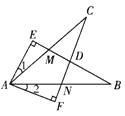
查看答案和解析>>【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论是_______.(写出正确答案的序号)
相关试题

