【题目】如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(﹣4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO. 
(1)求BC的长;
(2)求抛物线的解析式.
参考答案:
【答案】
(1)解:在Rt△AOB中,由勾股定理,得
AB= ![]() =2
=2 ![]() .
.
∵BC⊥AB,
∴∠ABC=∠AOB=90°,
∵∠CAB=∠BAO,
∴△CAB∽△BAO,
![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
BC= ![]()
(2)解:设C点坐标为(m,n),由勾股定理,
AC= ![]() =5.
=5.
AC2=25,BC2=5,
即  ,
,
解得m=﹣1,m=1(舍),n=4,
即C点坐标(﹣1,4).
将A,B,C点坐标代入函数解析式,得
 ,
,
解得  ,
,
抛物线的解析式为y=﹣ ![]() x2﹣
x2﹣ ![]() x+2
x+2
【解析】(1)根据勾股定理,可得AB的长,根据相似三角形的判定与性质,可得答案;(2)根据两点间的距离,可得两个方程,根据解方程,可得C点坐标,根据待定系数法,可得函数解析式.
【考点精析】根据题目的已知条件,利用抛物线与坐标轴的交点和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将点A先向右平移3个单位长度,在向下平移5个单位长度,得到A’;将点B先向下平移5个单位长度,再向右平移4个单位长度,得到B’,则A’与B’相距( )

A. 4个单位长度 B. 5个单位长度 C. 6个单位长度 D. 7个单位长度
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“互联网+”时代的到来,一种新型打车方式受到大众欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按
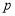 元/公里计算,耗时费按
元/公里计算,耗时费按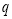 元/分钟计算(总费用不足
元/分钟计算(总费用不足 元按
元按 元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:
元计价).小敏、小刚两人用该打车方式出行,按上述计价规则,其行驶里程数、耗时以及打车总费用如下表:里程数
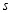 (公里)
(公里)耗时
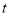 (分钟)
(分钟)车费(元)
小敏
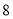
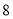

小刚
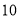

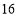
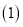 求
求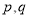 的值;
的值; 若小华也用该打车方式打车,平均车速为
若小华也用该打车方式打车,平均车速为 公里/时,行驶了
公里/时,行驶了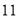
公里,那么小华的打车总费用为多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面的证明
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
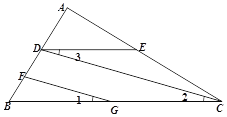
解:∵FG//CD (已知)
∴∠2=_________(____________________________)
又∵∠1=∠3,
∴∠3=∠2(等量代换)
∴BC//__________(_____________________________)
∴∠B+________=180°(______________________________)
又∵∠B=50°
∴∠BDE=________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,线段
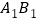 是由线段AB平移得到的,已知A、B两点的坐标分别为A(—2,3),B(—3,1)若
是由线段AB平移得到的,已知A、B两点的坐标分别为A(—2,3),B(—3,1)若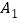 的坐标为(3,4).
的坐标为(3,4).(1)
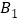 的坐标为 ;
的坐标为 ;(2)若线段AB上一点P的坐标为(
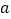 ,
,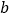 ),则点P的对应点
),则点P的对应点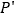 的坐标 .
的坐标 .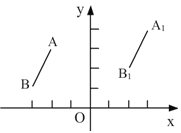
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有一组对角互补的凸四边形叫做“对补四边形”,性质:“对补四边形”一定是圆内接四边形.
(1)概念理解:请你根据上述描述定义举一个“对补四边形”的例子;
(2)问题探究:如图1,在对补四边形ABCD中,如果∠A=∠C,试探究AB、AD、BC、CD之间的数量关系,并说明理由;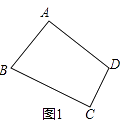
(3)应用拓展:如图2,在四边形ABCD中,AB≠BC,∠A=∠C=90°,连接BD,将△BCD沿BD折叠,得到△BFD.
①连接AF,四边形ABDF是对补四边形吗?请说明理由;
②若AB=1,BD=2,且BF把△ABD分成两个三角形的面积比为1:2,请求出CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC所在平面内找出一个点,使它与三角形中的任意两个顶点所组成的三角形都是等腰三角形。这样的点一共有( )
A. 1个 B. 4个 C. 7个 D. 10个
相关试题

