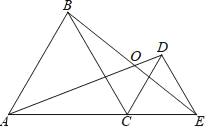
【题目】如图,△ABC和△CDE都是等边三角形,A、C、E在一条直线上.
(1)线段AD与BE相等吗?请证明你的结论;
(2)设AD与BE交于点O,求∠AOE的度数.
参考答案:
【答案】(1)AD=BE;(2)120°.
【解析】
(1) 利用等边三角形的性质得到一对角相等,一对边相等,利用等式的性质得到夹角相等,利用SAS得到三角形ACD与三角形BCE全等,利用全等三角形的对应边相等即可得证.
(2)利用三角形全等,转化相关角度即可解答.
解:(1)AD=BE,
理由如下:在等边△ABC和等边△CDE中,
∵∠ACB=∠DCE=60°,
∴∠ACD=∠BCE,
又∵AC=BC,CD=CE,
∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ACB=∠CBE+∠AEB=60°,
∴∠CAD+∠AEB=60°,
∴∠AOE=180°﹣(∠CAD+∠AEB)=120°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,关于此二次函数有以下四个结论:①a<0;②c>0;③b2﹣4ac>0;④ab>0,其中正确的有( )个.

A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读下面的材料并把解答过程补充完整.
问题:在关于
 ,
,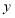 的二元一次方程组
的二元一次方程组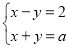 中,
中, ,
, ,求
,求 的取值范围.
的取值范围.在关于
 ,
,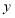 的二元一次方程组中,利用参数
的二元一次方程组中,利用参数 的代数式表示
的代数式表示 ,
,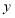 ,然后根据
,然后根据 ,
, 列出关于参数
列出关于参数 的不等式组即可求得
的不等式组即可求得 的取值范围.解:由
的取值范围.解:由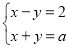 ,解得
,解得 ,又因为
,又因为 ,
, ,所以
,所以 解得____________.
解得____________.(2)请你按照上述方法,完成下列问题:
①已知
 ,且
,且 ,
, ,求
,求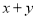 的取值范围;
的取值范围;②已知
 ,在关于
,在关于 ,
,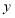 的二元一次方程组
的二元一次方程组 中,
中, ,
, ,请直接写出
,请直接写出 的取值范围(结果用含
的取值范围(结果用含 的式子表示)____________.
的式子表示)____________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装店用4500元购进一批衬衫,很快售完,服装店老板又用2100元购进第二批该款式的衬衫,进货量是第一次的一半,但进价每件比第一批降低了10元.
(1)这两次各购进这种衬衫多少件?
(2)若第一批衬衫的售价是200元/件,老板想让这两批衬衫售完后的总利润不低于1950元,则第二批衬衫每件至少要售多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
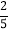 )2018×(﹣
)2018×(﹣ )2019×(﹣1)2017;
)2019×(﹣1)2017;(2)[(x﹣y)2+(x+y)(x﹣y)]÷2x;
(3)(x+2y﹣3)(x﹣2y+3);
(4)(1﹣
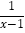 )÷
)÷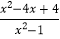 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某班40名学生的某次数学测验成绩统计表如下:

(1)若这个班的数学平均成绩是69分,求x和y的值;
(2)设此班40名学生成绩的众数为a分,中位数为b分,求(a-b)2的值;
(3)根据以上信息,你认为这个班的数学水平怎么样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】“校园安全”受到全社会的广泛关注,某校政教处对部分学生及家长就校园安全知识的了解程度,进行了随机抽样调查,并绘制成如图所示的两幅统计图,请根据统计图中的信息,解答下列问题:
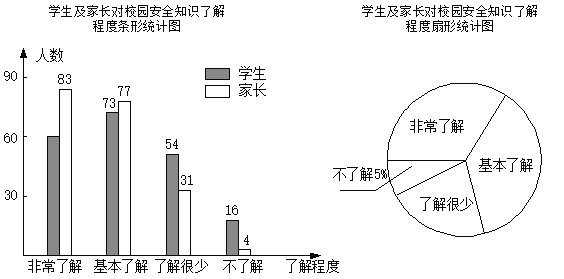
(1)参与调查的学生及家长共有 人;
(2)在扇形统计图中,“基本了解”所对应的圆心角的度数是 ;
(3)在条形统计图中,“非常了解”所对应的学生人数是 ;
(4)若全校有1200名学生,请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人.
相关试题

