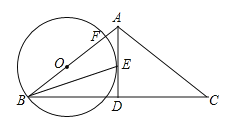
【题目】如图,在△ABC中,AB=AC,AD是角平分线,BE平分∠ABC交AD于点E,点O在AB上,以OB为半径的⊙O经过点E,交AB于点F.
(1)求证:AD是⊙O的切线;
(2)若AC=4,∠C=30°,求![]() 的长.
的长.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OE,利用角平分线的定义和圆的性质可得∠OBE=∠OEB=∠EBD,可证明OE∥BD,结合等腰三角形的性质可得AD⊥BD,可证得OE⊥AD,可证得AD为切线;
(2)利用(1)的结论,结合条件可求得∠AOE=30°,由AC的长可求得圆的半径,利用弧长公式可求得![]() .
.
试题解析:(1)证明:如图,连接OE,∵OB=OE,∴∠OBE=∠OEB,∵BE平分∠ABC,∴∠OBE=∠EBD,∴∠OEB=∠EBD,∴OE∥BD,∵AB=AC,AD平分∠BAC,∴AD⊥BC,∴∠OEA=∠BDA=90°,∴AD是⊙O的切线;
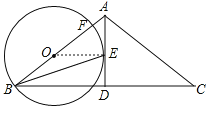
(2)解:∵AB=AC=4,∴OB=OE=OF=2,由(1)可知OE∥BC,且AB=AC,∴∠AOE=∠ABC=∠C=30°,∴![]() =
=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,后求值:
 ,其中x在数轴上的对应点到原点的距离为
,其中x在数轴上的对应点到原点的距离为  个单位长度.
个单位长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】方程x2=2x的根是( )
A.x=2
B.x=﹣2
C.x1=0,x2=2
D.x1=0,x2=﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】某班体育委员记录了第一小组七位同学定点投篮(每人投10个)的情况,投进篮框的个数为:6,10,5,3,4,8,4,这组数据的中位数和极差分别是( )
A. 4,7B. 7,5C. 5,7D. 3,7
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P、Q是反比例函数y=
 图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”)
图像上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 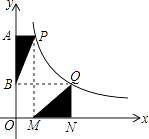
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列语句中属于命题的是( )
A. 作直线AB的平行线 B. 同旁内角相等 C. ∠1与∠2互余吗 D. 在线段AB上取点C
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,∠AOB、∠COD都是直角.
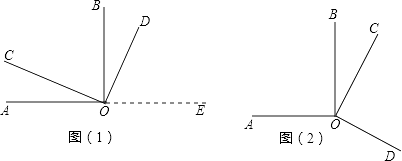
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
相关试题

