【题目】在等边△ABC的外侧作直线BD,作点A关于直线BD的对称点A′,连接AA′交直线BD于点E,连接A′C交直线BD于点F.
(1)依题意补全图1,已知∠ABD=30°,求∠BFC的度数; 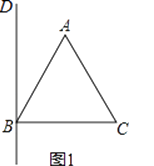
(2)如图2,若60°<∠ABD<90°,判断直线BD和A′C相交所成的锐角的度数是否为定值?若是,求出这个锐角的度数;若不是,请说明理由. 
参考答案:
【答案】
(1)解:补全的图1如下所示:
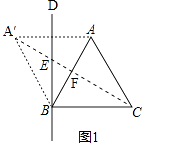
连接BA′,
∵由已知可得,BD垂直平分AA′,∠ABD=30°,△ABC是等边三角形,
∴△BA′A是等边三角形,AA′∥BC且AA′=BC,A′A=A′B,
∴四边形AA′BC是菱形,
∵∠ACB=60°,
∴∠BCE=30°
(2)解:直线BD和A′C相交所成的锐角的度数是定值,若下图所示,
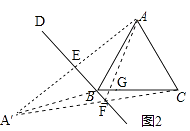
连接AF交BC于点G,
由已知可得,BA′=BA,BA=BC,FA′=FA,
则∠BA′A=∠BAA′,∠FA′A=∠FAA′,BA′=BC,
∴∠BA′C=∠BCA′,∠FA′B=∠FAB,
∴∠BCA′=∠FAB,
∵∠FGC=∠BGA,∠ABC=60°,
∴∠CFA=∠ABC=60°,
∵∠AFC+∠AFD+∠A′FD=180°,∠A′FD=∠AFD,
∴∠A′FD=60°,
即直线BD和A′C相交所成的锐角的度数是定值,这个锐角的度数是60°
【解析】(1)根据题意可以作出相应的图形,连接A′B,由题意可得到四边形AA′BC是菱形,根据菱形的对角线平分每一组对角,可以得到∠BFC的度数;(2)画出相应的图形,根据对称的性质可以得到相等的线段和相等的角,由等边△ABC,可以得到BC=BA,然后根据三角形内角和是180°,可以推出直线BD和A′C相交所成的锐角的度数,本题得以解决.
【考点精析】利用等边三角形的性质对题目进行判断即可得到答案,需要熟知等边三角形的三个角都相等并且每个角都是60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,M是铁丝AD的中点,将该铁丝首尾相接折成△ABC,且∠B=30°,∠C=100°,如图2.则下列说法正确的是( )
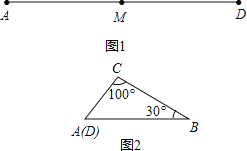
A. 点M在AB上
B. 点M在BC的中点处
C. 点M在BC上,且距点B较近,距点C较远
D. 点M在BC上,且距点C较近,距点B较远
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4m2﹣9n2= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示为一个污水净化塔内部,污水从上方入口进入后,流经形如等腰直角三角形的净化材枓表面,流向如图中箭头所示,每一次水流流经三角形两腰的机会相同,经过四层净化后流入底部的5个出口中的一个.下列判断:①5个出口的出水量相同;②2号出口的出水量与4号出口的出水量相同;③1,2,3号出水口的出水量之比约为1:4:6;④若净化材枓损耗的速度与流经其表面水的数量成正比,则更换最慢的一个三角形材枓使用的时间约为更换最快的一个三角形材枓使用时间的8倍.其中正确的判断有( )个.

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】三个连续正整数的和不大于12.这样的正整数有__________组.
-
科目: 来源: 题型:
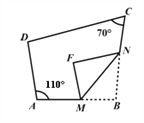
查看答案和解析>>【题目】如图,四边形ABCD中,点M、N分别在AB、BC上,将BMN沿MN翻折,得FMN,若MF∥AD,FN∥DC,则∠D的度数为_________
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各式:
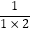 =
=  ﹣
﹣  ;
; 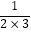 =
= 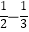 ;
; 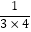 =
= 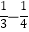 ;
; 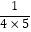 =
=  ﹣
﹣  ;….
;….
(1)猜想它的规律:把 表示出来:
表示出来:  =
=
(2)用你猜想得到的规律,计算: +
+  +
+ 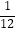 +
+ 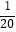 +…+
+…+ 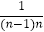 +
+  .
.
相关试题

