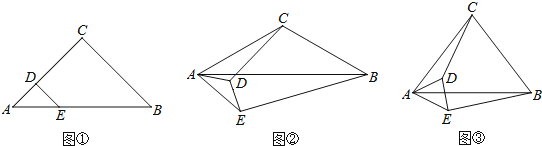
【题目】在△ABC中,CA=CB,在△AED中, DA=DE,点D、E分别在CA、AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,求CD与BE的数量关系;
(3)若∠ACB=∠ADE=2α(0°< α < 90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).
参考答案:
【答案】(1)BE=![]() CD;(2)BE=
CD;(2)BE=![]() CD;(3)BE=2CD·sinα,证明见解析.
CD;(3)BE=2CD·sinα,证明见解析.
【解析】试题分析:(1)由已知,△ADE和△ACB都是等腰直角三角形,所以有AE=![]() AD,AB=
AD,AB=![]() AC,从而有
AC,从而有![]() ,即BE=
,即BE=![]() CD.
CD.
(2)如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE=120°,
∴∠CAB=∠DAE,∠ACM=∠ADN="60°" ,AM=![]() AB,AN=
AB,AN=![]() AE.
AE.
∴∠CAD=∠BAE.
在Rt△ACM和Rt△ADN中,sin∠ACM=![]() =
=![]() ,sin∠ADN=
,sin∠ADN=![]() =
=![]() ,
,
∴![]() .∴
.∴![]() .
.
又∵∠CAD=∠BAE,∴△BAE∽△CAD.∴![]() .∴BE=
.∴BE=![]() CD.
CD.
(3)根据等腰三角形的性质和锐角三角函数定义求得![]() ,再由△BAE∽△CAD得出
,再由△BAE∽△CAD得出![]() ,从而得出结论.
,从而得出结论.
(1)BE=![]() CD.
CD.
(2)BE=![]() CD.
CD.
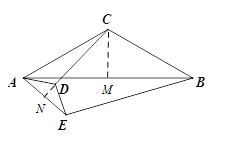
(3)BE=2CD·sinα.证明如下:
如图,分别过点C、D作CM⊥AB于点M,DN⊥AE于点N,
∵CA=CB,DA=DE,∠ACB=∠ADE="2α" ,
∴∠CAB=∠DAE,∠ACM=∠ADN="α" ,AM=![]() AB,AN=
AB,AN=![]() AE.
AE.
∴∠CAD=∠BAE.
在Rt△ACM和Rt△ADN中,sin∠ACM=![]() ,sin∠ADN=
,sin∠ADN=![]() ,
,
∴![]() .∴
.∴![]() .
.
又∵∠CAD=∠BAE,∴△BAE∽△CAD.∴![]() .
.
∴BE=2DC·sinα.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共用了18天完成全部任务.求原计划每天加工多少套运动服?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在式子“2×( )﹣6×( )=12”中括号内填入一个相同的数,使得等式成立,这个数是: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若规定收入为“+”,那么﹣50元表示( )
A.收入了50元
B.支出了50元
C.没有收入也没有支出
D.收入了100元 -
科目: 来源: 题型:
查看答案和解析>>【题目】2015年某企业按餐厨垃圾处理费50元/吨、建筑垃圾处理费20元/吨的收费标准,共支付餐厨和建筑垃圾处理费7000元.从2016年元月起,收费标准上调为:餐厨垃圾处理费120元/吨,建筑垃圾处理费40元/吨.若该企业2016年处理的这两种垃圾数量与2015年相比没有变化,就要多支付垃圾处理费8600元.
(1)该企业2015年处理的餐厨垃圾和建筑垃圾各多少吨?
(2)该企业计划2016年将上述两种垃圾处理总量减少到200吨,且建筑垃圾处理量不超过餐厨垃圾处理量的3倍,则2016年该企业最少需要支付这两种垃圾处理费共多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县2014年的GDP是250亿元,要使2016年的GDP达到360亿元,求这两年该县GDP年平均增长率.设年平均增长率为x,可列方程_____.
-
科目: 来源: 题型:
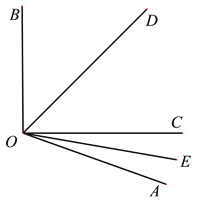
查看答案和解析>>【题目】如图,∠AOB=110°,OD平分∠BOC,OE平分∠AOC。
(1)求∠EOD的度数。
(2)若∠BOC=90°,求∠AOE的度数。
相关试题

