【题目】如图,已知O为直线AD上一点,射线OC,射线OB,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.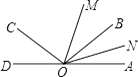
(1)∠COD与∠AOB相等吗?请说明理由;
(2)试求∠AOC与∠AOB的度数.
参考答案:
【答案】
(1)解:∵∠AOC与∠AOB互补,
∴∠AOC+∠AOB=180°,
∵∠AOC+∠DOC=180°,
∴∠COD=∠AOB;
(2)解:∵OM和ON分别是∠AOC和∠AOB的平分线,
∴∠AOM= ![]() ∠AOC,∠AON=
∠AOC,∠AON= ![]() ∠AOB,
∠AOB,
∴∠MON=∠AOM﹣∠AON= ![]() ∠AOC﹣
∠AOC﹣ ![]() ∠AOB=
∠AOB= ![]() (∠AOC﹣∠AOB)=
(∠AOC﹣∠AOB)= ![]() ∠BOC,
∠BOC,
∵∠MON=40°,
∴∠BOC=80°,
∴∠DOC+∠AOB=180°﹣80°=100°,
∵∠AOB=∠COD,
∴∠AOB=50°,
∴∠AOC=180°﹣∠COD=130°.
【解析】(1)根据题意可表示出∠AOC+∠AOB=180°,∠AOC+∠DOC=180°,由同角的补角相等可得答案;
(2)由OM和ON分别是∠AOC和∠AOB的平分线,可得到∠MON=![]() ∠BOC,进而求得∠BOC的度数,继而可得∠DOC+∠AOB的度数,再由(1)知,∠AOB=∠COD,则可得∠AOB的度数,又∠AOC=180°﹣∠COD可求出∠AOC的度数.
∠BOC,进而求得∠BOC的度数,继而可得∠DOC+∠AOB的度数,再由(1)知,∠AOB=∠COD,则可得∠AOB的度数,又∠AOC=180°﹣∠COD可求出∠AOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R .对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点.在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣
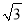 ,﹣1),C(
,﹣1),C(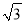 ,﹣1).
,﹣1).(1)已知点D(2,2),E(
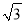 ,1),F(
,1),F(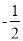 ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是 ;(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°.
①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为
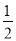 .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
-
科目: 来源: 题型:
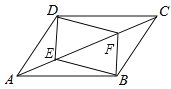
查看答案和解析>>【题目】如图,在ABCD中,点E,F在对角线AC上,且AE=CF.求证:
(1)DE=BF;
(2)四边形DEBF是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )
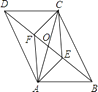
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA、OB分别是线段MC、MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短可为( )
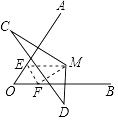
A.12cm
B.10cm
C.7cm
D.5cm -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2﹣y2=14,x﹣y=7,则x+y=
相关试题

