【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
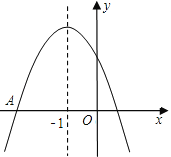
A.1个 B.2个 C.3个 D.4个
参考答案:
【答案】B
【解析】
试题分析:由抛物线的开口向下知a<0,与y轴的交点在y轴的正半轴上得到c>0,由对称轴为x=![]() =﹣1可以判定②错误,由图象与x轴有交点,对称轴为x=
=﹣1可以判定②错误,由图象与x轴有交点,对称轴为x=![]() =﹣1,与y轴的交点在y轴的正半轴上,可以推出b2﹣4ac>0,即b2>4ac,①正确,由x=﹣1时y有最大值,由图象可知y≠0,③错误,然后即可作出选择.
=﹣1,与y轴的交点在y轴的正半轴上,可以推出b2﹣4ac>0,即b2>4ac,①正确,由x=﹣1时y有最大值,由图象可知y≠0,③错误,然后即可作出选择.
解:①∵图象与x轴有交点,对称轴为x=![]() =﹣1,与y轴的交点在y轴的正半轴上,
=﹣1,与y轴的交点在y轴的正半轴上,
又∵二次函数的图象是抛物线,
∴与x轴有两个交点,
∴b2﹣4ac>0,
即b2>4ac,故本选项正确,
②∵抛物线的开口向下,
∴a<0,
∵与y轴的交点在y轴的正半轴上,
∴c>0,
∵对称轴为x=![]() =﹣1,
=﹣1,
∴2a=b,
∴2a+b=4a,a≠0,
故本选项错误,
③∵x=﹣1时y有最大值,
由图象可知y≠0,故本选项错误,
④把x=1,x=﹣3代入解析式得a+b+c=0,9a﹣3b+c=0,
两边相加整理得5a﹣b=﹣c<0,即5a<b,故本选项正确.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的括号里:﹣2.5,
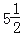 ,0,8,﹣2,
,0,8,﹣2,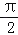 ,0.7,
,0.7,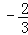 ,﹣1.121121112…,
,﹣1.121121112…,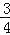 ,0.
,0.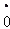
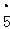 .
.正数集合{ …};
负数集合{ …};
整数集合{ …};
有理数集合{ …};
无理数集合{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
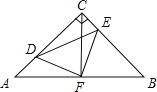
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.
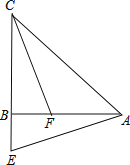
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(﹣23)+(﹣12)
(2)
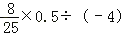
(3)1+(﹣2)+|﹣3|﹣5
(4)(﹣4)×2×(﹣0.25)
(5)
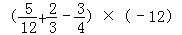
(6)
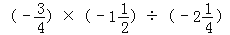
(7)(﹣
 )×42﹣0.25×(﹣8)×(﹣1)2011
)×42﹣0.25×(﹣8)×(﹣1)2011(8)﹣22﹣6÷(﹣2)×
 ﹣|﹣9+5|
﹣|﹣9+5| -
科目: 来源: 题型:
查看答案和解析>>【题目】等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;

(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2),当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
相关试题

