【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF.
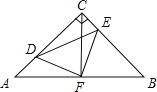
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
试题分析:(1)根据在等腰直角△ABC中,∠ACB=90°,AC=BC,利用F是AB中点,∠A=∠FCE=∠ACF=45°,即可证明:△ADF≌△CEF.
(2)利用△ADF≌△CEF,∠AFD+∠DFC=∠CFE+∠DFC,和∠AFC=90°即可证明△DFE是等腰直角三角形.
证明:(1)在等腰直角△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
又∵F是AB中点,
∴∠ACF=∠FCB=45°,
即,∠A=∠FCE=∠ACF=45°,且AF=CF,
在△ADF与△CEF中,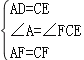 ,
,
∴△ADF≌△CEF(SAS);
(2)由(1)可知△ADF≌△CEF,
∴DF=FE,
∴△DFE是等腰三角形,
又∵∠AFD=∠CFE,
∴∠AFD+∠DFC=∠CFE+∠DFC,
∴∠AFC=∠DFE,
∵∠AFC=90°,
∴∠DFE=90°,
∴△DFE是等腰直角三角形.
-
科目: 来源: 题型:
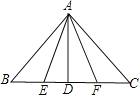
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:弦AB把圆周分成1:5的两部分,这弦AB所对应的圆周角的度数为
-
科目: 来源: 题型:
查看答案和解析>>【题目】将下列各数填入相应的括号里:﹣2.5,
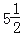 ,0,8,﹣2,
,0,8,﹣2,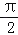 ,0.7,
,0.7,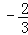 ,﹣1.121121112…,
,﹣1.121121112…,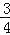 ,0.
,0.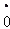
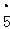 .
.正数集合{ …};
负数集合{ …};
整数集合{ …};
有理数集合{ …};
无理数集合{ …}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1035张照片,如果全班有x名同学,根据题意,列出方程为
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确的有( )
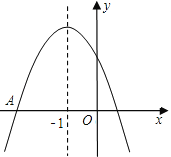
A.1个 B.2个 C.3个 D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.
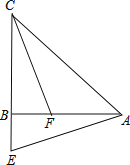
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=60°,求∠ACF的度数.
相关试题

