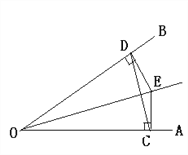
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)ED=EC;
(2)∠ECD=∠EDC;
(3)射线OE与CD有什么关系?(直接写出结果)
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)OE是线段CD的垂直平分线.
【解析】分析:(1)由E为∠AOB的平分线上一点,EC⊥OA,ED⊥OB,根据角平分线的性质,可证得ED=EC,∠OED=∠OEC,继而可证得EC=ED;(2)根据角平分线上的点到角的两边距离相等可得EC=DE,再根据等边对等角证明即可;(3) 利用“HL”证明Rt△OCE和Rt△ODE全等,根据全等三角形对应边相等可得OC=OD,然后根据等腰三角形三线合一证明.
证明:(1)∵点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴∠DOE=∠COE,∠ODE=∠OCE=90°,OE=OE,∴△OED≌△OEC(AAS),∴EC=ED;
(2)∵OE平分∠AOB,EC⊥OA,ED⊥OB,∴ED=EC,即△CDE为等腰三角形,
∴∠ECD=∠EDC;
(3)∵OC=OD,且DE=EC,∴OE是线段CD的垂直平分线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1). 36-76+(-23)-105 (2).(-301)+125+301+(-75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,直线
中,直线 与
与 轴交于点
轴交于点 ,与直线
,与直线 交于点
交于点 ,点
,点 的坐标为
的坐标为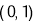

(1)求直线
 的解析式;
的解析式;(2)直线
 与
与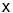 轴交于点
轴交于点 ,若点
,若点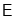 是直线
是直线 上一动点(不与点
上一动点(不与点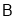 重合),当
重合),当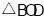 与
与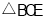 相似时,求点
相似时,求点 的坐标
的坐标 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫作点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,这样依次得到点A1,A2,A3,A4…,若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】以
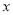 为自变量的二次函数
为自变量的二次函数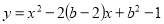 的图象不经过第三象限,则实数
的图象不经过第三象限,则实数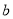 的取值范围是
的取值范围是A.
 B.
B.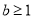 或
或 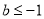 C.
C.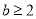 D.
D. 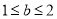
-
科目: 来源: 题型:
查看答案和解析>>【题目】[c-(a2)2]2等于( )
A. c -a2 B. c2 -2a4c+a8 C. c2 -a2 D. c2 -a4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班7名学生的数学考试成绩(单位:分)如下:52,76,80,76,71,92,67则这组数据的中位数是( ).
A.76.5分
B.71分
C.76分
D.80分
相关试题

