【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,点
,点![]() 的坐标为
的坐标为![]()

(1)求直线![]() 的解析式;
的解析式;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,若点
,若点![]() 是直线
是直线![]() 上一动点(不与点
上一动点(不与点![]() 重合),当
重合),当![]() 与
与![]() 相似时,求点
相似时,求点![]() 的坐标
的坐标
参考答案:
【答案】(1)![]() ;(2)(3,
;(2)(3,![]() ),(2,2).
),(2,2).
【解析】
试题分析:(1)首先设出一次函数解析式,将点A,D代入即可求出一次函数解析式;(2)先写出OB,OD,BC的长度,然后分两种情况讨论1:△BOD∽△BCE;2:△BOD∽△BEC.
试题解析:(1)设直线AD的解析式为y=kx+b
将点A![]() 代入直线y=kx+b中得:
代入直线y=kx+b中得:
解得:![]()
![]() 直经AD的解析式为:
直经AD的解析式为:![]()
(2)设点E的坐标为(m,![]() m+1)
m+1)
令![]() 得x=-2
得x=-2
![]() 点B的坐标为(-2,0)
点B的坐标为(-2,0)
令y=-x+3=0得x=3
![]() 点C的坐标为(3,0)
点C的坐标为(3,0)
![]() OB=2, OD=1, BC=5, BD=
OB=2, OD=1, BC=5, BD=![]()
1. 当△BOD∽△BCE时,如图(1)所示,过点C作CE![]() BC交直线AB于E:
BC交直线AB于E:
![]()
![]()
![]()
![]() CE=
CE=![]()
![]()
![]() m+1=
m+1=![]() ,解得m=3
,解得m=3
![]() 此时E点的坐标为(3,
此时E点的坐标为(3,![]() )
)

2. △BOD∽△BEC时,如图(2)所示,过点E作EF![]() BC于F点,则:
BC于F点,则:
![]()
![]()
![]()
![]() CE=
CE=![]()
![]() BE=
BE=![]()
![]()
![]() BE*CE=
BE*CE=![]() EF*BC
EF*BC
![]()
![]()
![]() EF=2
EF=2
![]()
![]() 解得m=2
解得m=2
![]() 此时E点的坐标为(2,2)
此时E点的坐标为(2,2)
![]() 当△BOD与△BCE相似时,满足条件的E坐标(3,
当△BOD与△BCE相似时,满足条件的E坐标(3,![]() ),(2,2).
),(2,2).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C为△ABD外接圆上的一动点(点C不在
 上,且不与点B,D重合),∠ACB=∠ABD=45°.
上,且不与点B,D重合),∠ACB=∠ABD=45°.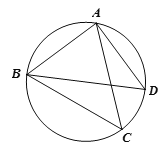
(1)求证:BD是该外接圆的直径;
(2)连结CD,求证:
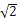 AC=BC+CD;
AC=BC+CD;(3)若△ABC关于直线AB的对称图形为△ABM,连接DM,试探究
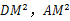 ,
,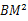 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】某银行办储蓄业务:取出950元,存入500元,取出800元,存入1200元,取出1025元,存入2500元,取出200元,请你计算一下,银行的现款增加了多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1). 36-76+(-23)-105 (2).(-301)+125+301+(-75)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫作点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,这样依次得到点A1,A2,A3,A4…,若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
-
科目: 来源: 题型:
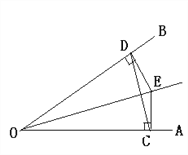
查看答案和解析>>【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)ED=EC;
(2)∠ECD=∠EDC;
(3)射线OE与CD有什么关系?(直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】以
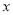 为自变量的二次函数
为自变量的二次函数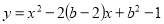 的图象不经过第三象限,则实数
的图象不经过第三象限,则实数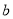 的取值范围是
的取值范围是A.
 B.
B.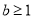 或
或 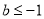 C.
C.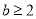 D.
D. 
相关试题

