【题目】阅读理解:在以后你的学习中,我们会学习一个定理:直角三角形斜边上的中线等于斜边的一半,即:如图1,在Rt△ABC中,∠ACB=90°,若点D是斜边AB的中点,则CD=![]() AB.
AB.

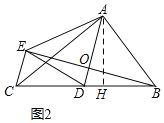
灵活应用:如图2,△ABC中,∠BAC=90°,AB=3, AC=4,点D是BC的中点,将△ABD沿AD翻折得到△AED,连接BE, CE.
(1)求AD的长;
(2)判断△BCE的形状;
(3)求CE的长.
参考答案:
【答案】(1)AD=![]() ;(2)见解析;(3)CE=
;(2)见解析;(3)CE=![]()
【解析】
(1)依据勾股定理进行计算即可得到BC的长,再根据直角三角形斜边上中线的性质即可得到结论;
(2)依据CD=DE=DB,可得∠DEC=∠DCE,∠DEB=∠DBE,再根据三角形内角和定理,即可得出∠DEB+∠DEC=90°,进而得到△BCE是直角三角形;
(3)利用![]() BCAH=
BCAH=![]() ABAC,可得AH=
ABAC,可得AH=![]() ,依据AD垂直平分线段BE,可得
,依据AD垂直平分线段BE,可得![]() ADBO=
ADBO=![]() BDAH,即可得出OB=
BDAH,即可得出OB=![]() ,BE=2OB=
,BE=2OB=![]() ,最后在Rt△BCE中,运用勾股定理可得EC=
,最后在Rt△BCE中,运用勾股定理可得EC=![]() .
.
(1)在Rt△ABC中,∠BAC=90°,AB=3,AC=4,
由勾股定理得,BC=![]() =5,
=5,
∵点D是BC的中点,BCRt△ABC的斜边,
∴AD=![]() BC=
BC=![]() ;
;
(2)△BCE为直角三角形.理由:
∵D是BC的中点
∴CD=BD
∵将△ABD沿AD翻折得到△AED,
∴DE=DB,
∴CD=DE=DB,
∴∠DEC=∠DCE,∠DEB=∠DBE,
∵∠DEC+∠DCE+∠DEB+∠DBE=180°,
∴∠DEB+∠DEC=90°,
∴∠BEC=90°,
∴△BCE是直角三角形;
(3)如图,连接BE交AD于O,作AH⊥BC于H.
由题可得AD=DC=DB=![]() ,
,
∵![]() BCAH=
BCAH=![]() ABAC,
ABAC,
∴AH=![]() ,
,
∵AE=AB,DE=DB,
∴点A在BE的垂直平分线上,点D在BE的垂直平分线上,
∴AD垂直平分线段BE,
∵![]() ADBO=
ADBO=![]() BDAH,
BDAH,
∴OB=![]() ,
,
∴BE=2OB=![]() ,
,
在Rt△BCE中,EC=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某养猪专业户利用一堵砖墙(长度足够)围成一个长方形猪栏,围猪栏的栅栏一共长40m,设这个长方形的相邻两边的长分别为x(m)和y(m).
(1)求y关于x的函数表达式和自变量的取值范围;
(2)若长方形猪栏砖墙部分的长度为5m,求自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P,Q是直线y=﹣
 上的两点,P在Q的左侧,且满足OP=OQ,OP⊥OQ,则点P的坐标是_____.
上的两点,P在Q的左侧,且满足OP=OQ,OP⊥OQ,则点P的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出△ABC 关于 y 轴对称的△A1B1C1并写出坐标;
(2)求出△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6),与直线OA相交于点A且点A的纵坐标为2, 动点P沿路线
 运动.
运动.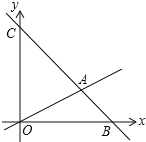
(1)求直线BC的解析式;
(2)在y轴上找一点M,使得△MAB的周长最小,则点M的坐标为______;(请直接写出结果)
(3)当△OPC的面积是△OAC的面积的
 时,求出这时P的坐标.
时,求出这时P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一圆柱,其高为12cm,它的底面半径为3cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,则蚂蚁经过的最短距离为_________.(π取3)

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读探索
问题背景:著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次”谈话“的语言.2002年8月在北京召开的国际数学大会会标取材于我国古代数学家赵爽的《勾股圆方图注》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图1所示).勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.
赵爽证明方法如下:
以a、b为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角三角形的面积等于
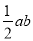 ,把这四个直角三角形拼成如图1所示形状.
,把这四个直角三角形拼成如图1所示形状.
∵Rt△DAE≌Rt△ABF
∴∠EDA=∠FAB
∵∠EAD+∠EDA=90°
∴∠FAB+∠EAD=90°
∴四边形ABCD是一个边长为c的正方形,它的面积等于
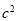
∵EF=FG=GH=HE=b-a
∠HEF=90°
∴四边形EFGH是一个边长为b-a的正方形,它的面积等于

∴
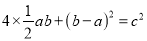
∴
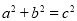 从而证明了勾股定理.
从而证明了勾股定理.思维拓展:
1、如果大正方形的面积为13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么
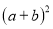 的值为 .
的值为 .2、美国第二十届总统加菲尔德也曾经给出了勾股定理的一种证明方法,如图2所示,
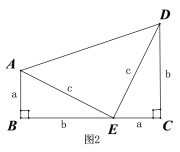
他用两个全等的直角三角形和一个等腰直角三角形拼出了一个直角梯形,请你利用此图形验证勾股定理.
证明:∵直角梯形ABCD的面积可以用两种方法表示:
第一种方法表示为:
第二种方法表示为:
∴ =
∴
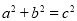
探索创新:
用纸做成四个全等的直角三角形,两直角边的长分别为a和b,斜边长为c,请你开动脑筋,将它们拼成一个能证明勾股定理的图形(不同于上面图1和图2).请画出你拼成的图形,并用你画的图形证明勾股定理.

相关试题

