【题目】如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
参考答案:
【答案】
(1)
解:如图1,
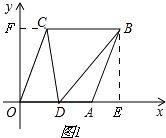
∵A(6,0),B(8,6),
∴FC=AE=8﹣6=2,OF=BE=6
∴C(2,6);
(2)
解:设D(x,0),当△ODC的面积是△ABD的面积的3倍时,
若点D在线段OA上,
∵OD=3AD,
∴ ![]() ×6x=3×
×6x=3× ![]() ×6(6﹣x),
×6(6﹣x),
∴x= ![]() ,
,
∴D( ![]() ,0);
,0);
若点D在线段OA延长线上,
∵OD=3AD,
∴ ![]() ×6x=3×
×6x=3× ![]() ×6(x﹣6),
×6(x﹣6),
∴x=9,
∴D(9,0)
(3)
解:如图2.
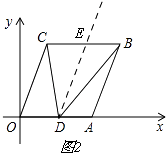
过点D作DE∥OC,
由平移的性质知OC∥AB.
∴OC∥AB∥DE.
∴∠OCD=∠CDE,∠EDB=∠DBA.
若点D在线段OA上,
∠CDB=∠CDE+∠EDB=∠OCD+∠DBA,
即α+β=θ;
若点D在线段OA延长线上,
∠CDB=∠CDE﹣∠EDB=∠OCD﹣∠DBA,
即α﹣β=θ.
【解析】(1)由点的坐标的特点,确定出FC=2,OF=6,得出C(2,6);(2)分点D在线段OA和在OA延长线两种情况进行计算;(3)分点D在线段OA上时,α+β=θ和在OA延长线α﹣β=θ两种情况进行计算;
【考点精析】本题主要考查了三角形的“三线”和三角形的面积的相关知识点,需要掌握1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内;三角形的面积=1/2×底×高才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD⊥CD,CD⊥BC,AC平分∠BAD.
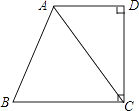
(1)求证:∠ACB=∠BAC;
(2)若∠B=80°,求∠DCA的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某新型感冒病毒的直径约为0.000000823米,将0.000000823用科学记数法表示为( )
A. 8.23×10﹣6 B. 8.23×10﹣7 C. 8.23×106 D. 8.23×107
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的内角和等于1260°,它是几边形?有多少条对角线?
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为20 cm的细绳围成一个等腰三角形,能围成有一边的长是5 cm的等腰三角形吗?如果能,求出其他两边的长;如果不能,说明理由
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一次函数的图象经过点(1,2),且y随x的增大而减小,则这个函数的表达式可能是
A. y=-2x+4 B. y=3x-1 C. y=-3x+1 D. y=2x+4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b(k<0)与反比例函数
 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
相关试题

