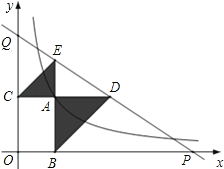
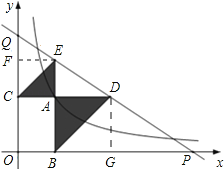
【题目】如图,已知动点A在函数![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC.直线DE分别交x,y轴分别于点P,Q.当QE:DP=4:9时,图中阴影部分的面积等于 .
参考答案:
【答案】![]()
【解析】
试题分析:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.令A(t,![]() ),则AD=AB=DG=
),则AD=AB=DG=![]() ,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积=
,AE=AC=EF=t,则图中阴影部分的面积=△ACE的面积+△ABD的面积=![]() t2+
t2+![]() ×
×![]() ,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=
,因此只需求出t2的值即可.先在直角△ADE中,由勾股定理,得出DE=![]() ,再由△EFQ∽△DAE,求出QE=
,再由△EFQ∽△DAE,求出QE=![]() ,△ADE∽△GPD,求出DP=:
,△ADE∽△GPD,求出DP=:![]() ,然后根据QE:DP=4:9,即可得出t2=
,然后根据QE:DP=4:9,即可得出t2=![]() .
.
解:解法一:过点D作DG⊥x轴于点G,过点E作EF⊥y轴于点F.
令A(t,![]() ),则AD=AB=DG=
),则AD=AB=DG=![]() ,AE=AC=EF=t.
,AE=AC=EF=t.
在直角△ADE中,由勾股定理,得DE=![]() =
=![]() =
=![]() =
=![]() .
.
∵△EFQ∽△DAE,
∴QE:DE=EF:AD,
∴QE=![]() ,
,
∵△ADE∽△GPD,
∴DE:PD=AE:DG,
∴DP=![]() .
.
又∵QE:DP=4:9,
∴![]() :
:![]() =4:9,
=4:9,
解得t2=![]() .
.
∴图中阴影部分的面积=![]() AC2+
AC2+![]() AB2=
AB2=![]() t2+
t2+![]() ×
×![]() =
=![]() +3=
+3=![]() ;
;
解法二:∵QE:DP=4:9,
∴EF:PG=4:9,
设EF=4t,则PG=9t,
∴A(4t,![]() ),
),
由AC=AE AD=AB,
∴AE=4t,AD=![]() ,DG=
,DG=![]() ,GP=9t,
,GP=9t,
∵△ADE∽△GPD,
∴AE:DG=AD:GP,
4t:![]() =
=![]() :9t,即t2=
:9t,即t2=![]() ,
,
图中阴影部分的面积=![]() 4t×4t+
4t×4t+![]() ×
×![]() ×
×![]() =
=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在; ④使得M=1的x值是
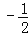 或
或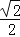 .
.其中正确的是( )
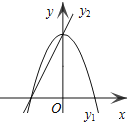
A.①② B.①④ C.②③ D.③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
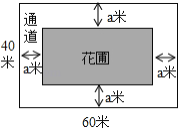
(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中, A、B两点分别在x轴、y轴的正半轴上,且OB = OA=3.(1)、求点A、B的坐标;(2)、已知点C(-2,2),求△BOC的面积;(3)、点P是第一象限角平分线上一点,若
 ,求点P的坐标.
,求点P的坐标.
-
科目: 来源: 题型:
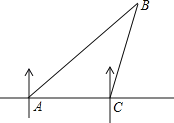
查看答案和解析>>【题目】一船在A处测得北偏东45°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P为直线m外一点,点A,B,C为直线m上三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线m的距离为( )
A. 4cm B. 2cm C. 小于2cm D. 不大于2cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一组数据:3,5,x,7,9的平均数为6,则x= .
相关试题

