【题目】某单位认真开展学习和实践科学发展观活动,在阶段总结中提出对本单位今后的整改措施,并在征求职工对整改方案的满意程度时进行民主测评,测评等级为:很满意、较满意、满意、不满意四个等级.

(1)若测评后结果如扇形图(图①),且测试等级为很满意、较满意、满意、不满意的人数之比为2:5:4:1,则图中a= ° ,β= °.
(2)若测试后部分统计结果如直方图(图②),请将直方图补画完整,并求出该单位职工总人数为 人.
(3)按上级要求,满意度必须不少于95%方案才能通过,否则,必须对方案进行完善.若要使该方案完善后能获得通过,至少还需增加 人对该方案的测评等级达满意(含满意)以上.
参考答案:
【答案】(1)120,30;(2)300 ,图详见解析;(3)10
【解析】
(1)用360°乘以份数占总份数的百分比即可求得两角的度数;
(2)首先根据满意的频数为100,然后求得总人数,最后根据份数求得每个小组的频数即可;
(3)设还需增加x人可以达到95%,根据题意列出方程求解即可.
(1)α=360°×![]() =120°,β=360°×
=120°,β=360°×![]() =30°,
=30°,
故答案为:120,30;
(2)观察统计图知满意的有100人,
故总人数为:100÷![]() =300人,
=300人,
很满意的有300×![]() =50人,
=50人,
较满意的有:300×![]() =125人,
=125人,
不满意的有:300×![]() =25人,
=25人,
统计图为:

(3)设还需增加x人可以达到95%,
根据题意得:![]() =95%,
=95%,
解得:x=10人,
故还需增加10人,才能达到95%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG交于点H,∠C=∠EFG,∠CED=∠GHD.
(1)求证:AB∥CD;
(2)若∠EHF=80°,∠D=40°,求∠AEM的度数。

-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读了其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①
 ,
,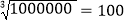 ,又
,又 ,
,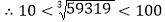 ,
, 能确定59319的立方根是个两位数.
能确定59319的立方根是个两位数.②
 59319的个位数是9,又
59319的个位数是9,又 ,
, 能确定59319的立方根的个位数是9.
能确定59319的立方根的个位数是9.③如果划去59319后面的三位319得到数59,
而
 ,则
,则 ,可得
,可得 ,
,由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数110592,按这种方法求立方根,请完成下列填空.
①它的立方根是 位数.
②它的立方根的个位数是 .
③它的立方根的十位数是 .
④110592的立方根是 .
(2)请直接填写结果:
①
 ;
;②
 ;
; -
科目: 来源: 题型:
查看答案和解析>>【题目】为了贯彻落实健康第一的指导思想,促进学生全面发展,国家每年都要对中学生进行一次体能测试,测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题
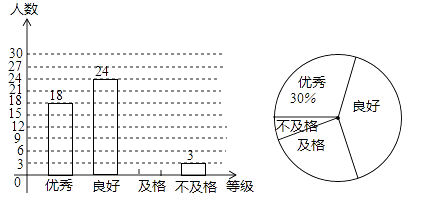
(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?
(5)请你对“不及格”等级的同学提一个友善的建议(一句话即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知P(1,1).过点P分别向x轴和y轴作垂线,垂足分别为A,B.
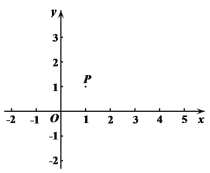
(1)点Q在直线AP上且与点P 的距离为2,则点Q的坐标为 ,三角形BPQ的面积是______;
(2)平移三角形ABP,若顶点P平移后的对应点为
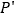 (4,3),
(4,3), ①画出平移后的三角形
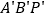 ;
;②直接写出四边形
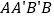 的面积为 .
的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A
必然事件
随机事件
m的值
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是
 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.
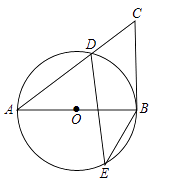
(1)求证:BC为⊙O的切线.
(2)若sinA=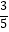 ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.
相关试题

