【题目】如图,在⊙O中,AB为直径,D、E为圆上两点,C为圆外一点,且∠E+∠C=90°.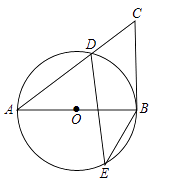
(1)求证:BC为⊙O的切线.
(2)若sinA= ![]() ,BC=6,求⊙O的半径.
,BC=6,求⊙O的半径.
参考答案:
【答案】
(1)证明:∵∠A与∠E所对的弧是 弧BD![]() ,
,
∴∠A=∠E,
又∵∠E+∠C=90°,
∴∠A+∠C=90°,
∴∠ABC=180°﹣90°=90°,
∵AB为直径,
∴BC为⊙O的切线.
(2)解:∵sinA= ![]() ,BC=6,
,BC=6,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴AC=10,
在Rt△ABC中,
∴AB= ![]() =
= ![]() =8,
=8,
又∵AB为直径,
∴⊙O的半径是 ![]() ×8=4.
×8=4.
【解析】(1)根据同弧所对的圆周角相等得∠A=∠E,同等量代换得∠A+∠C=90°,再由三角形内角和得∠ABC=90°,根据切线的判定即可得BC为⊙O的切线.
(2)由三角函数正弦定义得:sinA=![]() =
=![]() ,从而得AC=10,在Rt△ABC中,根据勾股定理得AB=8,从而得⊙O的半径.
,从而得AC=10,在Rt△ABC中,根据勾股定理得AB=8,从而得⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位认真开展学习和实践科学发展观活动,在阶段总结中提出对本单位今后的整改措施,并在征求职工对整改方案的满意程度时进行民主测评,测评等级为:很满意、较满意、满意、不满意四个等级.

(1)若测评后结果如扇形图(图①),且测试等级为很满意、较满意、满意、不满意的人数之比为2:5:4:1,则图中a= ° ,β= °.
(2)若测试后部分统计结果如直方图(图②),请将直方图补画完整,并求出该单位职工总人数为 人.
(3)按上级要求,满意度必须不少于95%方案才能通过,否则,必须对方案进行完善.若要使该方案完善后能获得通过,至少还需增加 人对该方案的测评等级达满意(含满意)以上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,已知P(1,1).过点P分别向x轴和y轴作垂线,垂足分别为A,B.
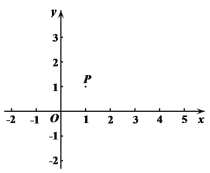
(1)点Q在直线AP上且与点P 的距离为2,则点Q的坐标为 ,三角形BPQ的面积是______;
(2)平移三角形ABP,若顶点P平移后的对应点为
 (4,3),
(4,3), ①画出平移后的三角形
 ;
;②直接写出四边形
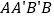 的面积为 .
的面积为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中装有颜色不同的8个小球,其中红球3个,黑球5个.
(1)先从袋中取出m(m>1)个红球,再从袋中随机摸出1个球,将“摸出黑球”记为事件A.请完成下列表格:
事件A
必然事件
随机事件
m的值
(2)先从袋中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个球是黑球的概率是
 ,求m的值.
,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,
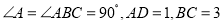 ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.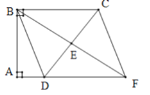
(1)求证:四边形BDFC是平行四边形;
(2)若△BCD是等腰三角形,求四边形BDFC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
的图象与x轴交于A(﹣1.0),B(3,0)两点,与y轴交于点C(0,﹣3),顶点为D.
(1)求此抛物线的解析式.
(2)求此抛物线顶点D的坐标和对称轴.
(3)探究对称轴上是否存在一点P,使得以点P、D、A为顶点的三角形是等腰三角形?若存在,请求出所有符合条件的P点的坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE.求证四边形AFCE为菱形,并求AF的长;
(2)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求t的值.
②若点P、Q的运动路程分别为a、b(单位:cm,ab≠0),已知A、C、P、Q四点为顶点的四边形是平行四边形,求a与b满足的数量关系式.

相关试题

