【题目】如图,在Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4,E是AB边的中点,F是AC边的中点。则EF=。
参考答案:
【答案】2
【解析】根据对称点的性质,延长FC到P , 使FC=PC , 连接EP交BC于D , 连接ED、FD , 此时ED+FD最小,即△EDF的周长最小,求出EP长,即可求出答案.
解答:∵E是AB边的中点,F是AC边的中点,
∴EF为△ABC的中位线,
∵BC=4,
∴EF= ![]() BC=
BC= ![]() ×4=2;
×4=2;
分析:根据对称点的性质,延长FC到P,使FC=PC,连接EP交BC于D,连接ED、FD,此时ED+FD最小,即△EDF的周长最小,求出EP长,即可求出答案.
【考点精析】关于本题考查的勾股定理的概念和三角形中位线定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中,是随机事件的是( )
A.射击运动员射击一次,命中靶心B.任意画一个三角形,其内角和是360°
C.掷一次骰子,向上一面的点数大于6D.通常加热到100℃,水沸腾
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下面不能判断是平行四边形的是( )
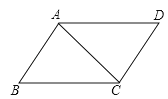
A.∠B=∠D,∠A=∠C
B.AB∥CD,AD∥BC
C.AB∥CD,AB=CD
D.∠B+∠DAB=180°,∠B+∠BCD=180° -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是由一些火柴棒搭成的图案:

(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某仓库某一天的原料进出记录如下表(运进用正数表示,运出用负数表示):
进出数量(吨)
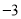
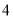


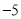
进出次数
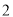
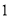
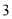
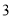
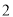
(
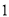 )这天仓库的原料比原来增加了还是减少了?请说明理由.
)这天仓库的原料比原来增加了还是减少了?请说明理由.(
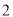 )根据实际情况,现有两种方案.
)根据实际情况,现有两种方案.方案一:运进每吨原料费用
 元,运出每吨原料费用
元,运出每吨原料费用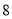 元.
元.方案二:不管运进还是运出费用都是每吨原料
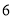 元.
元.从节约运费的角度考虑,选用哪一种方案比较合适.
(
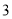 )在(
)在( )的条件下,若该仓库某个月运进原料共
)的条件下,若该仓库某个月运进原料共 吨,运出原料共
吨,运出原料共 吨,当
吨,当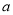 、
、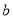 之间满足怎样的关系时两种方案吨运费相同.
之间满足怎样的关系时两种方案吨运费相同. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD , 要使得四边形ABCD是平行四边形,应添加的条件是 . (只填写一个条件,不得使用图形以外的字母和线段).

-
科目: 来源: 题型:
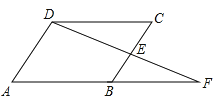
查看答案和解析>>【题目】如图,在四边形ABCD中,E是BC边的中点,连接DE并延长,交AB的延长线于F点,CD∥AF,请你添加一个条件:使四边形ABCD是平行四边形。
相关试题

