【题目】计算题
(1)计算:﹣(2﹣ ![]() )﹣(π﹣3.14)0+(1﹣cos30°)×(
)﹣(π﹣3.14)0+(1﹣cos30°)×( ![]() )﹣2;
)﹣2;
(2)先化简,再求值: ![]() ﹣
﹣ ![]() ÷
÷ ![]() ,其中a=
,其中a= ![]() .
.
参考答案:
【答案】
(1)
解:﹣(2﹣ ![]() )﹣(π﹣3.14)0+(1﹣cos30°)×(
)﹣(π﹣3.14)0+(1﹣cos30°)×( ![]() )﹣2
)﹣2
= ![]() ﹣2﹣1+(1﹣
﹣2﹣1+(1﹣ ![]() )×4
)×4
= ![]()
= ![]()
(2)
解: ![]() ﹣
﹣ ![]() ÷
÷ ![]()
= ![]()
= ![]()
= ![]()
= ![]() ,
,
当a= ![]() 时,原式=
时,原式= ![]()
【解析】(1)根据去括号得法则、零指数幂、特殊角的三角函数值、负整数指数幂可以解答本题;(2)根据分式的除法和减法可以化简题目中的式子,然后将a的值代入即可解答本题.
【考点精析】通过灵活运用零指数幂法则和整数指数幂的运算性质,掌握零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论: ①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )
A.①②③
B.③④⑤
C.①②④
D.①④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,经过点A的双曲线y=
 (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为  ,∠AOB=∠OBA=45°,则k的值为 .
,∠AOB=∠OBA=45°,则k的值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.
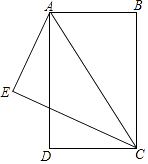
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 , 可使四边形ABCD为矩形.请加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市为创建全国文明城市,开展“美化绿化城市”活动,计划经过若干年使城区绿化总面积新增360万平方米.自2013年初开始实施后,实际每年绿化面积是原计划的1.6倍,这样可提前4年完成任务.
(1)问实际每年绿化面积多少万平方米?
(2)为加大创城力度,市政府决定从2016年起加快绿化速度,要求不超过2年完成,那么实际平均每年绿化面积至少还要增加多少万平方米?
相关试题

