【题目】如图,在平面直角坐标系中,经过点A的双曲线y= ![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为 ![]() ,∠AOB=∠OBA=45°,则k的值为 .
,∠AOB=∠OBA=45°,则k的值为 . 
参考答案:
【答案】1+ ![]()
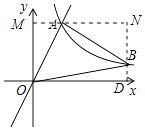
【解析】解:过A作AM⊥y轴于M,过B作BD选择x轴于D,直线BD与AM交于点N,如图所示: 则OD=MN,DN=OM,∠AMO=∠BNA=90°,
∴∠AOM+∠OAM=90°,
∵∠AOB=∠OBA=45°,
∴OA=BA,∠OAB=90°,
∴∠OAM+∠BAN=90°,
∴∠AOM=∠BAN,
在△AOM和△BAN中, 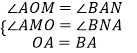 ,
,
∴△AOM≌△BAN(AAS),
∴AM=BN= ![]() ,OM=AN=
,OM=AN= ![]() ,
,
∴OD= ![]() +
+ ![]() ,OD=BD=
,OD=BD= ![]() ﹣
﹣ ![]() ,
,
∴B( ![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]() ),
),
∴双曲线y= ![]() (x>0)同时经过点A和B,
(x>0)同时经过点A和B,
∴( ![]() +
+ ![]() )(
)( ![]() ﹣
﹣ ![]() )=k,
)=k,
整理得:k2﹣2k﹣4=0,
解得:k=1± ![]() (负值舍去),
(负值舍去),
∴k=1+ ![]() ;
;
所以答案是:1+ ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=60°,点O从A点出发,以2m/s的速度沿∠BAC的角平分线向右运动,在运动过程中,以O为圆心的圆始终保持与∠BAC的两边相切,设⊙O的面积为S(cm2),则⊙O的面积S与圆心O运动的时间t(s)的函数图象大致为( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论: ①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )
A.①②③
B.③④⑤
C.①②④
D.①④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AB=CD,AD∥BC,以点B为圆心,BA为半径的圆弧与BC交于点E,四边形AECD是平行四边形,AB=6,则扇形(图中阴影部分)的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)计算:﹣(2﹣ )﹣(π﹣3.14)0+(1﹣cos30°)×(
)﹣(π﹣3.14)0+(1﹣cos30°)×(  )﹣2;
)﹣2;
(2)先化简,再求值: ﹣
﹣  ÷
÷ 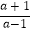 ,其中a=
,其中a=  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BA=AE=DC,AD=EC,CE⊥AE,垂足为E.
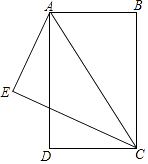
(1)求证:△DCA≌△EAC;
(2)只需添加一个条件,即 , 可使四边形ABCD为矩形.请加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】若n是一个两位正整数,且n的个位数字大于十位数字,则称n为“两位递增数”(如13,35,56等).在某次数学趣味活动中,每位参加者需从由数字1,2,3,4,5,6构成的所有的“两位递增数”中随机抽取1个数,且只能抽取一次.
(1)写出所有个位数字是5的“两位递增数”;
(2)请用列表法或树状图,求抽取的“两位递增数”的个位数字与十位数字之积能被10整除的概率.
相关试题

