【题目】如图,已知∠1=∠2=90°,AD=AE,那么图中有_____对全等三角形.

参考答案:
【答案】3
【解析】根据题意,结合图形,可得知△AEB≌△ADC,△BED≌△CDE,△BOD≌△COE.做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找.
解:①△AEB≌△ADC;∵AE=AD,∠1=∠2=90°,∠A=∠A,∴△AEC≌△ADC;∴AB=AC,∴BD=CE;
②△BED≌△CDE;∵AD=AE,∴∠ADE=∠AED,∵∠ADC=∠AEB,∴∠CDE=∠BED,
∴△BED≌△CDE.
③∵BD=CE,∠DBO=∠ECO,∠BOD=∠COE,∴△BOD≌△COE.
故答案为3.
“点睛”本题重点考查了三角形全等的判定定理,普通两个三角形全等共有四个定理,即AAS、ASA、SAS、SSS,直角三角形可用HL定理,但AAA、SSA,无法证明三角形全等,本题是一道较为简单的题目.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(4,0),与y轴交于C(0,﹣2).
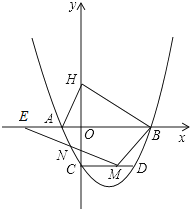
(1)求抛物线的解析式;
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号内.
15;0.81;-
 ,﹣3;﹣3.1;17;0;3.14
,﹣3;﹣3.1;17;0;3.14 正数集合{_______________________};
负数集合{_______};
整数集合{_________};
分数集合{_______________________};
有理数集合{_____________________}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

-
科目: 来源: 题型:
查看答案和解析>>【题目】有 20 筐白菜,以每筐 25 千克为标准,超过或不足的分别用正、负来表示,记录如下:

(1)与标准质量比较,20 筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价 2 .6 元,则出售这 20 筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
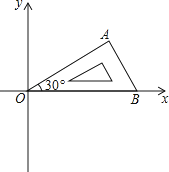
A.(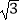 ,﹣1)
,﹣1)
B.(1,﹣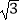 )
)
C.(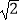 ,﹣
,﹣ 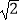 )
)
D.(﹣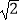 ,
, 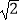 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.

相关试题

