【题目】将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( ) 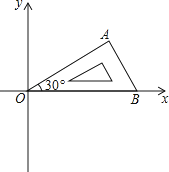
A.( ![]() ,﹣1)
,﹣1)
B.(1,﹣ ![]() )
)
C.( ![]() ,﹣
,﹣ ![]() )
)
D.(﹣ ![]() ,
, ![]() )
)
参考答案:
【答案】C
【解析】解:如图所示:过点A′作A′C⊥OB.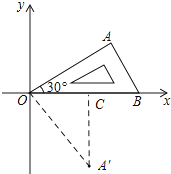
∵将三角板绕原点O顺时针旋转75°,
∴∠AOA′=75°,OA′=OA.
∴∠COA′=45°.
∴OC=2× ![]() =
= ![]() ,CA′=2×
,CA′=2× ![]() =
= ![]() .∴A′的坐标为(
.∴A′的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
故选:C.
先根据题意画出点A′的位置,然后过点A′作A′C⊥OB,接下来依据旋转的定义和性质可得到OA′的长和∠COA′的度数,最后依据特殊锐角三角函数值求解即可.本题主要考查的是旋转的定义和性质、特殊锐角三角函数值的应用,得到∠COA′=45°是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2=90°,AD=AE,那么图中有_____对全等三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】有 20 筐白菜,以每筐 25 千克为标准,超过或不足的分别用正、负来表示,记录如下:

(1)与标准质量比较,20 筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价 2 .6 元,则出售这 20 筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
-
科目: 来源: 题型:
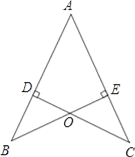
查看答案和解析>>【题目】如图,AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证:AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
相关试题

