【题目】如图,已知抛物线与x轴交于A(﹣1,0),B(4,0),与y轴交于C(0,﹣2).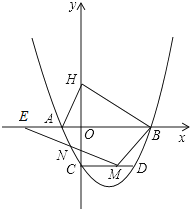
(1)求抛物线的解析式;
(2)H是C关于x轴的对称点,P是抛物线上的一点,当△PBH与△AOC相似时,求符合条件的P点的坐标(求出两点即可);
(3)过点C作CD∥AB,CD交抛物线于点D,点M是线段CD上的一动点,作直线MN与线段AC交于点N,与x轴交于点E,且∠BME=∠BDC,当CN的值最大时,求点E的坐标.
参考答案:
【答案】
(1)
解:∵抛物线与x轴交于A(﹣1,0),B(4,0),
∴设抛物线的解析式为:y=a(x+1)(x﹣4),
把(0,﹣2)代入y=a(x+1)(x﹣4),
∴a= ![]() ,
,
∴抛物线的解析式为:y= ![]() x2﹣
x2﹣ ![]() x﹣2
x﹣2
(2)
解:当△PBH与△AOC相似时,
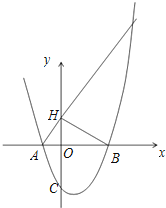
∴△AOC是直角三角形,
∴△PBH也是直角三角形,
由题意知:H(0,2),
∴OH=2,
∵A(﹣1,0),B(4,0),
∴OA=1,OB=4,
∴ ![]()
∵∠AOH=∠BOH,
∴△AOH∽△BOH,
∴∠AHO=∠HBO,
∴∠AHO+∠BHO=∠HBO+∠BHO=90°,
∴∠AHB=90°,
设直线AH的解析式为:y=kx+b,
把A(﹣1,0)和H(0,2)代入y=kx+b,
∴ ![]() ,
,
∴解得 ![]() ,
,
∴直线AH的解析式为:y=2x+2,
联立 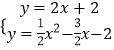 ,
,
解得:x=1或x=﹣8,
当x=﹣1时,
y=0,
当x=8时,
y=18
∴P的坐标为(﹣1,0)或(8,18)
(3)
解:过点M作MF⊥x轴于点F,
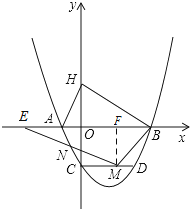
设点E的坐标为(n,0),M的坐标为(m,0),
∵∠BME=∠BDC,
∴∠EMC+∠BME=∠BDC+∠MBD,
∴∠EMC=∠MBD,
∵CD∥x轴,
∴D的纵坐标为﹣2,
令y=﹣2代入y= ![]() x2﹣
x2﹣ ![]() x﹣2,
x﹣2,
∴x=0或x=3,
∴D(3,﹣2),
∵B(4,0),
∴由勾股定理可求得:BD= ![]() ,
,
∵M(m,0),
∴MD=3﹣m,CM=m(0≤m≤3)
∴由抛物线的对称性可知:∠NCM=∠BDC,
∴△NCM∽△MDB,
∴ ![]() ,
,
∴ ![]() ,
,
∴CN= ![]() =﹣
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
∴当m= ![]() 时,CN可取得最大值,
时,CN可取得最大值,
∴此时M的坐标为( ![]() ,﹣2),
,﹣2),
∴MF=2,BF= ![]() ,MD=
,MD= ![]()
∴由勾股定理可求得:MB= ![]() ,
,
∵E(n,0),
∴EB=4﹣n,
∵CD∥x轴,
∴∠NMC=∠BEM,∠EBM=∠BMD,
∴△EMB∽△BDM,
∴ ![]() ,
,
∴MB2=MDEB,
∴ ![]() =
= ![]() ×(4﹣n),
×(4﹣n),
∴n=﹣ ![]() ,
,
∴E的坐标为(﹣ ![]() ,0).
,0).
【解析】(1)设抛物线的解析式为y=a(x+1)(x﹣4),然后将(0,﹣2)代入解析式即可求出a的值;(2)当△PBH与△AOC相似时,△PBH是直角三角形,由 ![]() 可知∠AHB=90°,所以求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m=
可知∠AHB=90°,所以求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m= ![]() 时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.本题考查函数的综合问题,涉及待定系数法求解析式,联立解析式求交点坐标,相似三角形判定与性质,二次函数最值等知识,内容较为综合,需要学生灵活运用知识去解决问题.
时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.本题考查函数的综合问题,涉及待定系数法求解析式,联立解析式求交点坐标,相似三角形判定与性质,二次函数最值等知识,内容较为综合,需要学生灵活运用知识去解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中有全等三角形( )

A. 5对; B. 4对; C. 3对; D. 2对
-
科目: 来源: 题型:
查看答案和解析>>【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
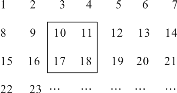
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填在相应的大括号内.
15;0.81;-
 ,﹣3;﹣3.1;17;0;3.14
,﹣3;﹣3.1;17;0;3.14 正数集合{_______________________};
负数集合{_______};
整数集合{_________};
分数集合{_______________________};
有理数集合{_____________________}.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个长方形操场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为r米,广场的长为a米,宽为b米.
(1)请列式表示操场空地的面积;
(2)若休闲广场的长为 50米,宽为20米,圆形花坛的半径为 3米,求操场空地的面积.(π取 3.14,计算结果保留 0.1)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2=90°,AD=AE,那么图中有_____对全等三角形.

相关试题

